题目内容
在△ABC中,点D在线段AC上,点E在BC上,且DE∥AB将△CDE绕点C按顺时针方向旋转得到△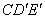 (使
(使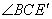 <180°),连接
<180°),连接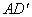 、
、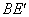 ,设直线
,设直线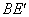 与AC交于点O.
与AC交于点O.
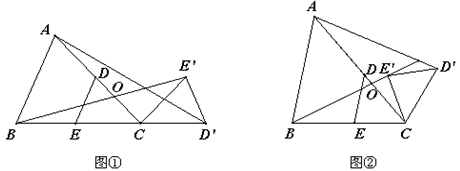
(1)如图①,当AC=BC时,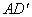 :
: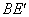 的值为______;
的值为______;
(2)如图②,当AC=5,BC=4时,求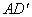 :
: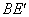 的值;
的值;
(3)在(2)的条件下,若∠ACB=60°,且E为BC的中点,求△OAB面积的最小值.
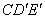 (使
(使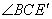 <180°),连接
<180°),连接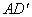 、
、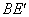 ,设直线
,设直线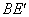 与AC交于点O.
与AC交于点O.
(1)如图①,当AC=BC时,
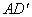 :
: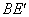 的值为______;
的值为______;(2)如图②,当AC=5,BC=4时,求
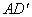 :
: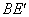 的值;
的值;(3)在(2)的条件下,若∠ACB=60°,且E为BC的中点,求△OAB面积的最小值.
(1)1(2)5:4(3)

试题分析: (1)1; 提示:△ACD′≌BCE′.
(2)解:∵DE∥AB,
∴△CDE∽△CAB.
∴
 .
.由旋转图形的性质得,
 ,
,∴
 .
.∵
 ,
,∴
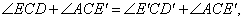 即
即 .
.∴
 ∽
∽ .
.∴
 .
.(3)解:作BM⊥AC于点M,则BM=BC·sin60°=2
 .
.∵E为BC中点,
∴CE=
 BC=2.
BC=2.△CDE旋转时,点
 在以点C为圆心、CE长为半径的圆上运动.
在以点C为圆心、CE长为半径的圆上运动.∵CO随着
 的增大而增大,
的增大而增大,∴当
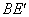 与⊙C相切时,即
与⊙C相切时,即 =90°时
=90°时 最大,
最大,则CO最大.
∴此时
 =30°,
=30°, =
= BC=2=CE.
BC=2=CE.∴点
 在AC上,即点
在AC上,即点 与点O重合.
与点O重合.∴CO=
 =2.
=2.又∵CO最大时,AO最小,且AO=AC-CO=3.
∴
 .
.点评:此类试题属于难度很大的综合性试题,考生在解答此类试题时要注意掌握好一些基本知识

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目


 轴对称的△A1B1C1,并写出△A1B1C1中顶点C1的坐标;
轴对称的△A1B1C1,并写出△A1B1C1中顶点C1的坐标;  .
. 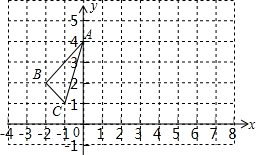
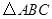 的顶点坐标分别为
的顶点坐标分别为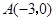 ,
,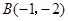 ,
,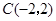 .
.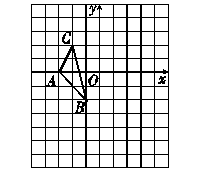
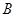 点顺时针旋转
点顺时针旋转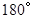 后的图形;
后的图形;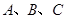 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点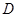 的坐标.
的坐标.