Question

【题目】最短路径问题：

例：如图所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距离之和最短．

解：只有A、C、B在一直线上时，才能使AC+BC最小．作点A关于直线“街道”的对称点A′，然后连接A′B，交“街道”于点C，则点C就是所求的点．

应用：已知：如图A是锐角∠MON内部任意一点，

在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小.

（1）借助直角三角板在下图中找出符合条件的点B和C.

（2）若∠MON=30°，OA=10,求三角形的最小周长。

Answer 1

【答案】(1)见解析；（2）10

【解析】试题分析： 作点关于的对称点，关于的对称点，连接,与相交于两点，连接, 即为所求．

试题解析： 作点关于的对称点，关于的对称点，连接,与相交于两点，连接, 即为所求．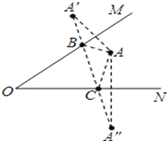

此时线段的长度即为周长的最小值

连接

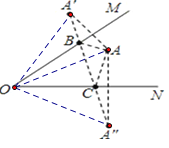
由对称性知：

为等边三角形

所以三角形的最小周长为10.