题目内容
二次函数y=ax2+bx+c图象上部分点的对应值如下表：| x | -3 | -2 | -1 | 1 | 2 | 3 | 4 | |
| y | 6 | -4 | -6 | -6 | -4 | 6 |
【答案】分析：由表中数据可知抛物线y=ax2+bx+c与x轴的交点为（-2，0）、（3，0），然后画出草图即可确定y＜0的是x的取值范围．
解答：
解：由表中数据可知抛物线y=ax2+bx+c与x轴的交点为（-2，0）、（3，0），
画出草图，可知使y＜0的x的取值范围为-2＜x＜3．
点评：观察二次函数的对应值的表格，关键是寻找对称点，顶点坐标及对称轴，利用对称性解答．
解答：
解：由表中数据可知抛物线y=ax2+bx+c与x轴的交点为（-2，0）、（3，0），画出草图，可知使y＜0的x的取值范围为-2＜x＜3．
点评：观察二次函数的对应值的表格，关键是寻找对称点，顶点坐标及对称轴，利用对称性解答．
练习册系列答案
通城学典默写能手系列答案
相关题目
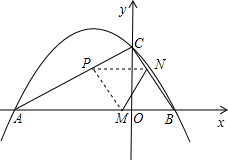点C
如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：①abc＞0；②2a+b=0；③a+b+c＞0；④当-1＜x＜3时，y＞0．其中正确结论的序号是
（2012•孝感）二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图所示．对于下列说法：