题目内容
 如图,BD是△ABC的角平分线,∠ABD=36°,∠C=72°,则图中的等腰三角形有
如图,BD是△ABC的角平分线,∠ABD=36°,∠C=72°,则图中的等腰三角形有
- A.0个
- B.1个
- C.2个
- D.3个
D
分析:由题意,推出∠ABC=72°,∠A=36°,∠DBC=36°,∠BDC=72°,推出△ABC、△ABD、△DBC为等腰三角形,所以,图中共有3个等腰三角形.
解答:∵BD是△ABC的角平分线,∠ABD=36°,
∴∠ABC=72°
∵∠C=72°,
∴∠A=36°,∠DBC=36°,∠BDC=72°,
∴△ABC、△ABD、△DBC为等腰三角形.
故选D.
点评:本题主要考查三角形的内角和定理、等腰三角形的判定和性质,关键在于根据三角形的内角和定理推出相关内角的度数.
分析:由题意,推出∠ABC=72°,∠A=36°,∠DBC=36°,∠BDC=72°,推出△ABC、△ABD、△DBC为等腰三角形,所以,图中共有3个等腰三角形.
解答:∵BD是△ABC的角平分线,∠ABD=36°,
∴∠ABC=72°
∵∠C=72°,
∴∠A=36°,∠DBC=36°,∠BDC=72°,
∴△ABC、△ABD、△DBC为等腰三角形.
故选D.
点评:本题主要考查三角形的内角和定理、等腰三角形的判定和性质,关键在于根据三角形的内角和定理推出相关内角的度数.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数.
25、如图,BD是△ABC的角平分线.已知∠1=∠A,∠2=∠3,求△ABC的各个内角的度数. 如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=
如图,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,AB=12,BC=15,S△ABD=36,则S△BCD=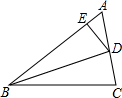 如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长.
如图,BD是∠ABC的平分线,DE⊥AB于E,S△ABC=90,AB=18,BC=12,求DE的长. 如图,BD是△ABC的角平分线,且BD=BC=AD.
如图,BD是△ABC的角平分线,且BD=BC=AD. 如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是
如图,BD是△ABC的中线,若△ABD的面积是10,则△ABC的面积是