题目内容
|x-12|+|x+y-25|与z2-10z+25互为相反数,那么以x、y、z为边的三角形是什么三角形?
解:z2-10z+25=(z-5)2,
∵|x-12|+|x+y-25|与z2-10z+25互为相反数,
∴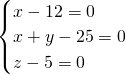 ,
,
解得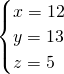 ,
,
∵52+122=132,
∴以x、y、z为边的三角形是直角三角形.
分析:首先根据非负数的性质可得x-12=0,x+y-25=0,z-5=0,再解方程可得a、b、c的值,然后根据勾股定理逆定理可判定出三角形的形状.
点评:此题主要考查了勾股定理逆定理,以及非负数的性质,关键是根据非负数的性质求出a、b、c的值.
∵|x-12|+|x+y-25|与z2-10z+25互为相反数,
∴
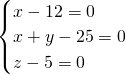 ,
,解得
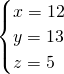 ,
,∵52+122=132,
∴以x、y、z为边的三角形是直角三角形.
分析:首先根据非负数的性质可得x-12=0,x+y-25=0,z-5=0,再解方程可得a、b、c的值,然后根据勾股定理逆定理可判定出三角形的形状.
点评:此题主要考查了勾股定理逆定理,以及非负数的性质,关键是根据非负数的性质求出a、b、c的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直角三角形两直角边长度为5,12,则斜边上的高( )
| A、6 | ||
| B、8 | ||
C、
| ||
D、
|
关于x的一元二次方程(a-1)x2+a2-1=0的一个根是x=0,则a等于( )
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、
|
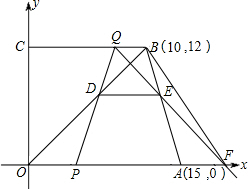 动时间为t(单位:秒).
动时间为t(单位:秒).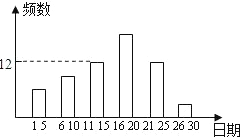 出一张卡片,抽到第四组作品的概率是多少?
出一张卡片,抽到第四组作品的概率是多少?