题目内容
 如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )
如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,则四边形DHFC的面积为( )A、
| ||
B、3
| ||
| C、9 | ||
D、6
|
考点:旋转的性质,正方形的性质
专题:计算题
分析:连结CH,根据旋转的性质得∠BCF=30°,则∠FCD=60°,根据“HL”可判断Rt△CFH≌Rt△CDH,则∠FCH=∠DCH=30°,在Rt△CFH中,根据含30度的直角三角形三边的关系得到HF=
=
,然后根据三角形面积公式计算出S△FCH=
,最后利用四边形DHFC的面积=2S△FCH即可.
| FC | ||
|
| 3 |
3
| ||
| 2 |
解答:解:连结CH,如图,
∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,
∴∠BCF=30°,
∴∠FCD=60°,
∵在Rt△CFH和Rt△CDH中
,
∴Rt△CFH≌Rt△CDH(HL),
∴∠FCH=∠DCH,
∴∠FCH=30°,
在Rt△CFH中,CF=3,∠FCH=30°,
∴HF=
=
,
∴S△FCH=
×3×
=
,
∴四边形DHFC的面积=2S△FCH=3
.
故选B.

∵正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,
∴∠BCF=30°,
∴∠FCD=60°,
∵在Rt△CFH和Rt△CDH中
|
∴Rt△CFH≌Rt△CDH(HL),
∴∠FCH=∠DCH,
∴∠FCH=30°,
在Rt△CFH中,CF=3,∠FCH=30°,
∴HF=
| FC | ||
|
| 3 |
∴S△FCH=
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
∴四边形DHFC的面积=2S△FCH=3
| 3 |
故选B.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质.

练习册系列答案
相关题目
 如图,将等腰直角△ABC沿斜边BC方向平移得到△A1B1C1.若AB=3,图中阴影部分面积为2,则BB1=
如图,将等腰直角△ABC沿斜边BC方向平移得到△A1B1C1.若AB=3,图中阴影部分面积为2,则BB1= 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35米的速度沿着与水平方向成75°角的方向飞行,40分钟时到达C处,此气球上的人发现气球与山顶P及小山西侧的B庄在一直线上,同时测得B庄的俯角为30°,又在A庄测处山顶P的仰角为45°.
如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35米的速度沿着与水平方向成75°角的方向飞行,40分钟时到达C处,此气球上的人发现气球与山顶P及小山西侧的B庄在一直线上,同时测得B庄的俯角为30°,又在A庄测处山顶P的仰角为45°. 已知:如图,在△ABC中,∠ABC=90°.DC⊥AC于点C,且CD=CA,DE⊥BC交BC的延长线于点E.
已知:如图,在△ABC中,∠ABC=90°.DC⊥AC于点C,且CD=CA,DE⊥BC交BC的延长线于点E.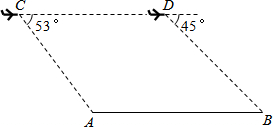 飞机测量一岛屿两端A、B的距离,在距海平面垂直高度为200m的点C处测得A的俯角为53°,然后沿着平行于AB的方向水平飞行了300m,在点D处测得B的俯角为45°,求岛屿两端A、B的距离.(参考数据:sin53°≈
飞机测量一岛屿两端A、B的距离,在距海平面垂直高度为200m的点C处测得A的俯角为53°,然后沿着平行于AB的方向水平飞行了300m,在点D处测得B的俯角为45°,求岛屿两端A、B的距离.(参考数据:sin53°≈