题目内容
如图是一个长为8m，宽为6 m，高为5 m的仓库，在其内壁的点A（长的四等分点）处有一只壁虎．在点B（宽的三等分点）处有一只蚊子．则壁虎爬到蚊子处的最短距离应为
- A.
m - B.
m - C.5
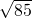m - D.13m
A
分析：将点A和点B所在的面展开，则为矩形，连接AB，分类探讨壁虎爬到蚊子处的距离，找到最短距离即可．
解答：
解：
①将正面和左面展开，过点B向底面作垂线，垂足为点C，则△ABC为直角三角形，
∵AC=
×8+
×6=8，BC=5，∴AB=
=
=，
故壁虎爬到蚊子处的最短距离为m．
②将正面和上面展开，则A到B的水平距离为6，垂直距离为7，
∴此时的最短距离为，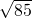
∵＞，
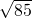故选A．
点评：本题的关键是将长方体展开，用勾股定理求出壁虎所走的最短距离．
分析：将点A和点B所在的面展开，则为矩形，连接AB，分类探讨壁虎爬到蚊子处的距离，找到最短距离即可．
解答：
解：①将正面和左面展开，过点B向底面作垂线，垂足为点C，则△ABC为直角三角形，
∵AC=
×8+×6=8，BC=5，∴AB===，故壁虎爬到蚊子处的最短距离为
m．②将正面和上面展开，则A到B的水平距离为6，垂直距离为7，
∴此时的最短距离为
，∵
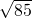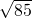＞，故选A．
点评：本题的关键是将长方体展开，用勾股定理求出壁虎所走的最短距离．
练习册系列答案
相关题目
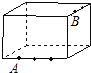如图是一个长为8m，宽为6 m，高为5 m的仓库，在其内壁的点A（长的四等分点）处有一只壁虎．在点B（宽的三等分点）处有一只蚊子．则壁虎爬到蚊子处的最短距离应为（ ）A、
| ||
B、
| ||
C、5
| ||
| D、13m |
如图是一个长8m、宽6m、高5m的仓库，在其内壁的点A（长的四等分点）处有一只壁虎、点B（宽的三等分点）处有一只蚊子．则壁虎爬到蚊子处的最短距离为
m
m
m
m
m
m