题目内容
 如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.(1)若∠AOB=90°,∠AOC=40°,求∠EOF的度数;
(2)若∠AOB=a,求∠EOF的度数;
(3)若将题中“平分”的条件改为“∠EOB=
| 1 |
| 3 |
| 2 |
| 3 |
分析:(1)首先根据角平分线的定义求得∠COF,然后求得∠BOC的度数,根据角平分线的定义求得∠EOC,然后根据∠EOF=∠COF+∠EOC求解;
(2)根据角平分线的定义可以得到∠COF=
∠AOC,∠EOC=
∠BOC,然后根据∴∠EOF=∠COF+∠EOC=
∠AOC+
∠BOC=
(∠AOC+∠BOC)即可得到;
(3))根据∠EOB=
∠COB,可以得到,∠EOC=
∠COB,则∠EOF=∠EOC+∠COF=
∠BOC+
∠AOC=
∠AOB,从而求解.
(2)根据角平分线的定义可以得到∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3))根据∠EOB=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:(1)∵OF平分∠AOC,
∴∠COF=
∠AOC=20°,
∵∠BOC=∠AOB-∠AOC=90°-40°=50°,OE平分∠BOC,
∴∠EOC=
∠BOC=25°
∴∠EOF=∠COF+∠EOC=45°;
(2))∵OF平分∠AOC,
∴∠COF=
∠AOC,
同理,∠EOC=
∠BOC,
∴∠EOF=∠COF+∠EOC=
∠AOC+
∠BOC=
(∠AOC+∠BOC)=
∠AOB=
a;
(3)∵∠EOB=
∠COB,
∴∠EOC=
∠COB,
∴∠EOF=∠EOC+∠COF=
∠BOC+
∠AOC=
∠AOB=
a.
∴∠COF=
| 1 |
| 2 |
∵∠BOC=∠AOB-∠AOC=90°-40°=50°,OE平分∠BOC,

∴∠EOC=
| 1 |
| 2 |
∴∠EOF=∠COF+∠EOC=45°;
(2))∵OF平分∠AOC,
∴∠COF=
| 1 |
| 2 |
同理,∠EOC=
| 1 |
| 2 |
∴∠EOF=∠COF+∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)∵∠EOB=
| 1 |
| 3 |
∴∠EOC=
| 2 |
| 3 |
∴∠EOF=∠EOC+∠COF=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了角平分线的性质,以及角度的计算,正确理解角平分线的定义是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目

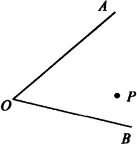
 如图,已知∠AOB内有一点P,过点P画MN∥OB交OA于C,过点P画PD⊥OA,垂足为D,并量出点P到OA距离.
如图,已知∠AOB内有一点P,过点P画MN∥OB交OA于C,过点P画PD⊥OA,垂足为D,并量出点P到OA距离.
