Question

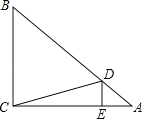
【题目】如图，平行四边形中，是的延长线上一点，与交于点，。

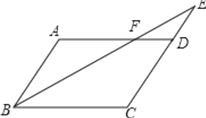
（1）求证：;

（2）若的面积为4，求平行四边形的面积。

Answer 1

【答案】（1）见解析；（2）48

【解析】

（1）根据平行四边形的对角相等，再根据AB∥CD，可得一对内错角相等，然后利用两组对应角相等即可证明△ABF∽△CEB；

（2）先证明△DEF∽△CEB，根据两三角形的相似比，求出△EBC的面积，也就求出了四边形BCDF的面积，再根据△DEF∽△ABF，求出△AFB的面积，由此可求出平行四边形ABCD的面积．

(1)证明：∵四边形ABCD是平行四边形，

∴∠A=∠C，AB∥CD，

∴∠ABF=∠CEB，

∴△ABF∽△CEB；

(2)∵四边形ABCD是平行四边形，

∴AD∥BC，AB平行且等于CD，

∴△DEF∽△CEB，△DEF∽△ABF，

∵CD=2DE，

∴,，

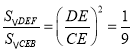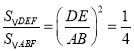∵S△DEF=4，

∴S△CEB=36，S△ABF=16，

∴S四边形BCDF=S△BCES△DEF=32，

∴S四边形ABCD=S四边形BCDF+S△ABF=32+16=48.