题目内容
 如图①所示,直线l:
如图①所示,直线l:| 4 | 3 |
(1)求直线n(未运动时)与直线m的函数解析式.
(2)请直接写出直线n运动至点C时的t值,并试求直线l与直线m之间的距离.
(3)如图②,当直线n运动到点c时,在点c右侧是否存在直线s:x=b,使得它与直线l、直线m与直线n所构成的四边形的面积为25.若存在,请求出直线s的函数解析式;若不存在,请说明理由.
分析:(1)先根据直线l的解析式求出点A、B的坐标,然后根据△ABO与△DAO相似,利用相似三角形对应边成比例列式求出OD的长度,从而得到点D的坐标,再根据两平行直线的解析式k值相等,利用待定系数法列式求解即可得到直线m、n的解析式;
(2)根据直线m的解析式求出点C的坐标,得到OC、OD的长度,然后利用勾股定理列式计算求出CD的长度,再根据速度是每秒1个单位求解t的值,在Rt△ACD中,利用勾股定理列式求出AD的长,即为直线l、m间的距离;
(3)假设存在直线s,先根据相似三角形对应边成比例列式求出AE、CE的长度,再根据直线l、m的解析式求出HG、HF的长度,然后根据所构成的四边形的面积=S△AGH-S△ACE-S△FCH,列式进行求解即可.
(2)根据直线m的解析式求出点C的坐标,得到OC、OD的长度,然后利用勾股定理列式计算求出CD的长度,再根据速度是每秒1个单位求解t的值,在Rt△ACD中,利用勾股定理列式求出AD的长,即为直线l、m间的距离;
(3)假设存在直线s,先根据相似三角形对应边成比例列式求出AE、CE的长度,再根据直线l、m的解析式求出HG、HF的长度,然后根据所构成的四边形的面积=S△AGH-S△ACE-S△FCH,列式进行求解即可.
解答:解:(1)当y=0时,
x+4=0,解得x=-3,
当x=0时,y=4,
∴点A、B的坐标为A(-3,0),B(0,4),
∴OA=3,OB=4,
∵△BAD为直角三角形,
∴AD⊥AB,
明显可得△ABO∽△DAO,
∴
=
,
即
=
,
解得OD=
,
∴点D的坐标为(0,-
),
设直线n的解析式为y=kx-
,
则-3k-
=0,
解得k=-
,
∴直线n的解析式为y=-
x-
,
∵直线m与l平行,且经过点D,
∴直线m的解析式为y=
x-
;
(2)当y=0时,
x-
=0,
解得x=
,
∴点C的坐标为(
,0),
∴OC=
,
∴CD=
=
=
,
∴t=CD÷1=
,
在Rt△ACD中,AC=3+
=
,
AD=
=
=
=
,
∴直线l、m间的距离为
;
(3)如图,假设存在直线s=b,
则CH=b-
,FH=
b-
,HG=
b+4,AH=b-(-3)=b+3,
∴S△FCH=
CH•FH=
(b-
)(
b-
),S△AGH=
AH•HG=
(b+3)(
b+4),
又∵由CE⊥AB,可得△ACE∽△ABO,
∴
=
=
,
即
=
=
,
解得AE=
,CE=
,
∴S△ACE=
AE•CE=
×
×
=
×
,
∴四边形的面积=S△AGH-S△ACE-S△FCH,
=
(b+3)(
b+4)-
×
-
(b-
)(
b-
)=25,
整理得,
b=
,
解得b=
,
∵
>
,
∴直线s在点C的右侧,
故存在直线s:x=
,使得它与直线l、直线m与直线n所构成的四边形的面积为25.
| 4 |
| 3 |
当x=0时,y=4,
∴点A、B的坐标为A(-3,0),B(0,4),
∴OA=3,OB=4,
∵△BAD为直角三角形,
∴AD⊥AB,
明显可得△ABO∽△DAO,
∴
| OA |
| OD |
| OB |
| OA |
即
| 3 |
| OD |
| 4 |
| 3 |
解得OD=
| 9 |
| 4 |
∴点D的坐标为(0,-
| 9 |
| 4 |
设直线n的解析式为y=kx-
| 9 |
| 4 |
则-3k-
| 9 |
| 4 |
解得k=-
| 3 |
| 4 |
∴直线n的解析式为y=-
| 3 |
| 4 |
| 9 |
| 4 |

∵直线m与l平行,且经过点D,
∴直线m的解析式为y=
| 4 |
| 3 |
| 9 |
| 4 |
(2)当y=0时,
| 4 |
| 3 |
| 9 |
| 4 |
解得x=
| 27 |
| 16 |
∴点C的坐标为(
| 27 |
| 16 |
∴OC=
| 27 |
| 16 |
∴CD=
| OD2+OC2 |
(
|
| 45 |
| 16 |
∴t=CD÷1=
| 45 |
| 16 |
在Rt△ACD中,AC=3+
| 27 |
| 16 |
| 75 |
| 16 |
AD=
| AC2-CD2 |
(
|
| 60 |
| 16 |
| 15 |
| 4 |
∴直线l、m间的距离为
| 15 |
| 4 |
(3)如图,假设存在直线s=b,
则CH=b-
| 27 |
| 16 |
| 4 |
| 3 |
| 9 |
| 4 |
| 4 |
| 3 |
∴S△FCH=
| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 16 |
| 4 |
| 3 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
又∵由CE⊥AB,可得△ACE∽△ABO,
∴
| OA |
| AE |
| OB |
| CE |
| AB |
| AC |
即
| 3 |
| AE |
| 4 |
| CE |
| 5 | ||
|
解得AE=
| 45 |
| 16 |
| 15 |
| 4 |
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 45 |
| 16 |
| 15 |
| 4 |
| 1 |
| 2 |
| 675 |
| 64 |
∴四边形的面积=S△AGH-S△ACE-S△FCH,
=
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 675 |
| 64 |
| 1 |
| 2 |
| 27 |
| 16 |
| 4 |
| 3 |
| 9 |
| 4 |
整理得,
| 25 |
| 2 |
| 1675 |
| 32 |
解得b=
| 67 |
| 16 |
∵
| 67 |
| 16 |
| 27 |
| 16 |
∴直线s在点C的右侧,
故存在直线s:x=
| 67 |
| 16 |
点评:本题综合考查了一次函数,坐标与图形的变化,待定系数法求直线解析式,两平行直线的k值相等,求解数据比较复杂,运算量较大,计算时要仔细认真,对运算能力要求比较高.

练习册系列答案
相关题目
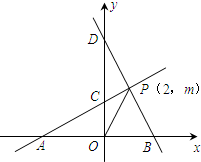 已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
已知,如图1所示,直线PA与x轴交于点A,与y轴交于点C(0,2),且S△AOC=4,直线BD与x轴交于点B,与y轴交于点D,直线PA与直线BD交于点P(2,m),点P在第一象限,连接OP.
 (1)如图1所示的射线上O为端点,A、B、C为任意三点,则图中有
(1)如图1所示的射线上O为端点,A、B、C为任意三点,则图中有
 、
、 被
被 、
、 所截,且
所截,且

 ,则
,则 _________
_________ .
.