题目内容
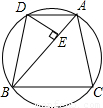
已知⊙O内接△ABC,⊙Q切AB,AC于E,F且与⊙O内切.试证:EF中点P是△ABC之内心.
 证明:如图,显然EF中点P、圆心Q,BC中点K都在∠BAC平分线上.
证明:如图,显然EF中点P、圆心Q,BC中点K都在∠BAC平分线上.易知AQ=
 .
.∵QK•AQ=MQ•QN,
∴QK=

=
 =sinα•(2R-r).
=sinα•(2R-r).由Rt△EPQ知PQ=sinα•r.
∴PK=PQ+QK=sinα•r+sinα•(2R-r)=sinα•2R.
∴PK=BK.α
利用内心等量关系之逆定理,
即知P是△ABC的内心.
分析:根据内切圆的性质可以得出EF中点P、圆心Q,BC中点K都在∠BAC平分线上,再利用相交弦定理表示出QK,再结合正弦定理运用两圆的半径表示出QK,
点评:此题主要考查了内心的有关知识与相交弦定理,以及余弦定理的应用和内心等量关系等知识.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
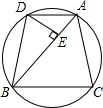 如图,已知圆内接△ABC中,AB>AC,D为
如图,已知圆内接△ABC中,AB>AC,D为
 的中点,DE⊥AB于E,求证:BD2-AD2=AB•AC.
的中点,DE⊥AB于E,求证:BD2-AD2=AB•AC.