题目内容
【题目】已知点A(1,a),B(m,n)(m>1)均在正比例函数y=2x的图象上,反比例函数y=![]() 的图象经过点A,过点B作BD⊥x轴于D,交反比例函数y=
的图象经过点A,过点B作BD⊥x轴于D,交反比例函数y=![]() 的图象于点C,连接AC,则下列结论正确的是( )
的图象于点C,连接AC,则下列结论正确的是( )
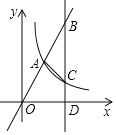
A.当m=2时,AC⊥OB
B.当AB=2OA时,BC=2CD
C.存在一个m,使得S△BOD=3S△OCD
D.四边形AODC的面积固定不变
【答案】C
【解析】
求出点A的坐标,确定函数关系式,进而求出各条线段的长,借助三角函数值和三角形的面积公式,逐个判断即可.
由题意知,点A的坐标为(1,2),则反比例函数的解析式为y=![]() ,
,
当m=2时,点B的坐标为(2,4),则点C的坐标为(2,1),BC=3,
∵AB=![]() ,OB=2
,OB=2![]() ,
,
∴cos∠OBD=![]() ,
,
∴AC与OB不垂直,故A错误;
当AB=2OA时,点B的横坐标为3,则点B的坐标为(3,6),点C的坐标为(3,![]() ),则BC=6﹣
),则BC=6﹣![]() =
=![]() ,则BC=8CD≠2CD,故B错误;
,则BC=8CD≠2CD,故B错误;
∵S△OCD=![]() k=
k=![]() ×2=1,
×2=1,
∴S△BOD=3=![]() ODBD=
ODBD=![]() m2m=m2,解得m=
m2m=m2,解得m=![]() (负值已舍去).
(负值已舍去).
即存在m,使得S△BOD=3S△COD,故C正确;
∵随着点B向右移动,点C到线段AB的距离逐渐增大,则△AOC的面积逐渐增大,而S△OCD=1固定不变,则四边形AODC的面积逐渐增大,故D错误.
故选:C.

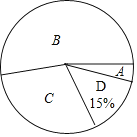
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.