题目内容
 如图,抛物线经过了边长为1的正方形ABOC的三个顶点A,B,C,则抛物线的解析式为________.
如图,抛物线经过了边长为1的正方形ABOC的三个顶点A,B,C,则抛物线的解析式为________.
y=- x2+
x2+
分析:本题可先根据正方形的边长求出A、B、C三点的坐标,然后用待定系数法求出抛物线的解析式.
解答: 解:连接BC,交OA于D,则BC⊥OA
解:连接BC,交OA于D,则BC⊥OA
在等腰Rt△OAB中,AB=1,∠BAO=∠AOB=45°
∴OA= ,OD=BD=CD=
,OD=BD=CD=
∴A、B、C三点的坐标分别是(0, )、(-
)、(- ,
, )、(
)、( ,
, )
)
设过A、B、C三点的函数解析式y=ax2+bx+c,可得
 ,解得
,解得
所以抛物线的解析式为:y=- x2+
x2+ .
.
点评:本题主要考查了二次函数解析式的确定以及正方形的性质,根据正方形的性质和边长求出A、B、C三点的坐标是解题的关键.
 x2+
x2+
分析:本题可先根据正方形的边长求出A、B、C三点的坐标,然后用待定系数法求出抛物线的解析式.
解答:
 解:连接BC,交OA于D,则BC⊥OA
解:连接BC,交OA于D,则BC⊥OA在等腰Rt△OAB中,AB=1,∠BAO=∠AOB=45°
∴OA=
 ,OD=BD=CD=
,OD=BD=CD=
∴A、B、C三点的坐标分别是(0,
 )、(-
)、(- ,
, )、(
)、( ,
, )
)设过A、B、C三点的函数解析式y=ax2+bx+c,可得
 ,解得
,解得
所以抛物线的解析式为:y=-
 x2+
x2+ .
.点评:本题主要考查了二次函数解析式的确定以及正方形的性质,根据正方形的性质和边长求出A、B、C三点的坐标是解题的关键.

练习册系列答案
相关题目
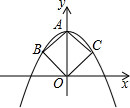 如图,抛物线经过了边长为1的正方形ABOC的三个顶点A,B,C,则抛物线的解析式为
如图,抛物线经过了边长为1的正方形ABOC的三个顶点A,B,C,则抛物线的解析式为