题目内容
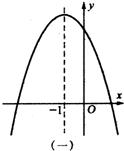
已知二次函数y=ax2+bx+c的图象如图所示，
是该抛物线的对称轴．根据图4所提供的信息，请你写出有关a，b，c的四条结论，并简单说明理由．
解：①∵开口方向向上，∴a＞0，
②∵与y轴的交点为在y轴的正半轴上，∴c＞0，
③∵对称轴为x=
＞0，∴a、b异号，即b＜0，
④∵抛物线与x轴有两个交点，∴b2-4ac＞0，
⑤当x=1时，y=a+b+c＜0，
⑥当x=-1时，y=a-b+c＞0．
结论有：a＞0，b＜0，c＜0，a+b+c＜0，a-b+c＞0等．
分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论．
点评：考查二次函数y=ax2+bx+c系数符号的确定．
②∵与y轴的交点为在y轴的正半轴上，∴c＞0，
③∵对称轴为x=
＞0，∴a、b异号，即b＜0，④∵抛物线与x轴有两个交点，∴b2-4ac＞0，
⑤当x=1时，y=a+b+c＜0，
⑥当x=-1时，y=a-b+c＞0．
结论有：a＞0，b＜0，c＜0，a+b+c＜0，a-b+c＞0等．
分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论．
点评：考查二次函数y=ax2+bx+c系数符号的确定．
练习册系列答案
阅读快车系列答案
相关题目
21、已知二次函数y=a（x+1）2+c的图象如图所示，则函数y=ax+c的图象只可能是（ ）
+bx+c的图象与x轴交于点A．B,与y轴交于点 C．
已知二次函数y=ax+bx+c（a≠0，a，b，c为常数），对称轴为直线x=1，它的部分自变量与函数值y的对应值如下表，写出方程ax2+bx+c=0的一个正数解的近似值________（精确到0.1）．
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |