Question

【题目】在四边形ABCD中，∠B=∠C=90°，AB=3，BC=4，CD=1．以AD为腰作等腰△ADE，使∠ADE=90°，过点E作EF⊥DC交直线CD于点F．请画出图形，并直接写出AF的长．

Answer 1

【答案】2或2

【解析】

如图，分两种情况讨论，E点可在AD的上方，由已知条件可证的△ADM≌△EDF，可得DF=DM，后可求得FN的长，可求得AF的长；

E点可在AD的下方，同理可证△ADN≌△DEF，可得DF=DM，可求得FN的长后的AF的长.

如图1中，作AN⊥CF于N，DM⊥AB于M．

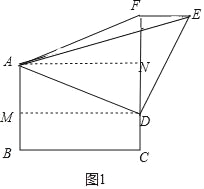
∵∠B=∠C=∠DMB=90°，

∴四边形BCDM是矩形，易证四边形AMDN是矩形，

∴CD=BM=1，AM=AB﹣BM=2，DM=BC=AN=4，DN=AM=2，

∵∠AMD=∠DFE，∠ADM=∠FDE，DA=DE，

∴△ADM≌△EDF，

∴DF=DM=4，

∴FN=DF﹣DN=2，

在Rt△AFN中，AF==2．

如图2中，作AN⊥FD交FD的延长线于N．

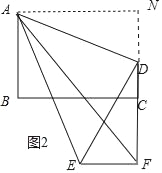
易证AN=BC=4，△ADN≌△DEF，

∴DF=AN=4，DN=CN﹣CD=2，

∴FN=6，

在Rt△AFN中，AF==2．