题目内容
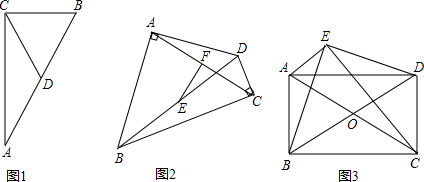
 如图,所示,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,求该四边形的面积.
如图,所示,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,求该四边形的面积.
分析:由AB=4,BC=3,∠B=90°可得AC=5.可求得S△ABC;再由AC=5,AD=13,CD=12,可得△ACD为直角三角形,进而求得S△ACD,可求S四边形ABCD=S△ABC+S△ACD.
解答:解:在Rt△ABC中,AB=4,BC=3,则有AC=
=5.
∴S△ABC=
AB•BC=
×4×3=6.
在△ACD中,AC=5,AD=13,CD=12.
∵AC2+CD2=52+122=169,AD2=132=169.
∴AC2+CD2=AD2,∴△ACD为直角三角形,
∴S△ACD=
AC•CD=
×5×12=30.
∴S四边形ABCD=S△ABC+S△ACD=6+30=36.
| AB2+BC2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACD中,AC=5,AD=13,CD=12.
∵AC2+CD2=52+122=169,AD2=132=169.
∴AC2+CD2=AD2,∴△ACD为直角三角形,
∴S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形ABCD=S△ABC+S△ACD=6+30=36.
点评:此题主要考查勾股定理和逆定理的应用,还涉及了三角形的面积计算.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
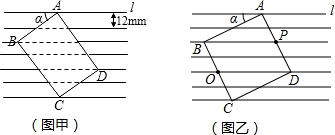
 (1)如图1,经历矩形性质的探索过程,你可以发现:直角三角形斜边上的中线等于斜边上的一半.如在Rt△ABC中CD是斜边AB的中线,则CD=
(1)如图1,经历矩形性质的探索过程,你可以发现:直角三角形斜边上的中线等于斜边上的一半.如在Rt△ABC中CD是斜边AB的中线,则CD=