题目内容
已知双曲线y= 与直线y=-x+1没有交点,则b的取值范围是________.
与直线y=-x+1没有交点,则b的取值范围是________.
b>
分析:根据方程解析式,可以得到 =-x+1,即可转化为一个一元二次方程,利用判别式求出b的取值范围.
=-x+1,即可转化为一个一元二次方程,利用判别式求出b的取值范围.
解答:因为双曲线y= 与直线y=-x+1没有交点,
与直线y=-x+1没有交点,
即方程 =-x+1无解,
=-x+1无解,
去分母,得x2-x+b=0,
∴△=b2-4ac=(-1)2-4×1×b=1-4b<0,
解得b> .
.
点评:考查一元二次方程根的判别式和双曲线与直线的位置关系,同时考查综合应用能力及推理能力.

分析:根据方程解析式,可以得到
 =-x+1,即可转化为一个一元二次方程,利用判别式求出b的取值范围.
=-x+1,即可转化为一个一元二次方程,利用判别式求出b的取值范围.解答:因为双曲线y=
 与直线y=-x+1没有交点,
与直线y=-x+1没有交点,即方程
 =-x+1无解,
=-x+1无解,去分母,得x2-x+b=0,
∴△=b2-4ac=(-1)2-4×1×b=1-4b<0,
解得b>
 .
.点评:考查一元二次方程根的判别式和双曲线与直线的位置关系,同时考查综合应用能力及推理能力.

练习册系列答案
相关题目
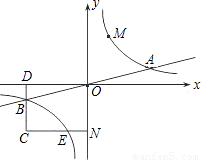
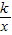 与直线y=
与直线y=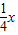 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=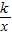 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=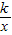 于点E,交BD于点C.
于点E,交BD于点C.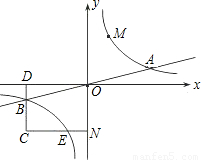
 与直线y=
与直线y= 相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A,B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=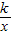 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=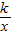 于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
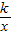 与直线y=
与直线y=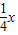 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=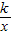 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=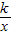 于点E,交BD于点C.
于点E,交BD于点C.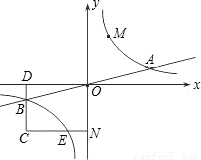
 与直线y=
与直线y=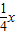 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=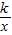 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=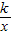 于点E,交BD于点C.
于点E,交BD于点C.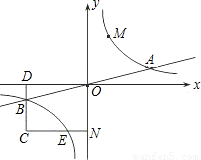
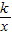 与直线y=
与直线y=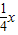 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线y=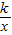 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线y=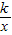 于点E,交BD于点C.
于点E,交BD于点C.