题目内容
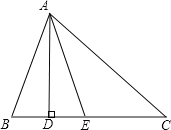
【题目】已知l1∥l2，点A，B在l1上，点C，D在l2上，连接AD，BC．AE，CE分别是∠BAD，∠BCD的角平分线，∠α＝70°，∠β＝30°．
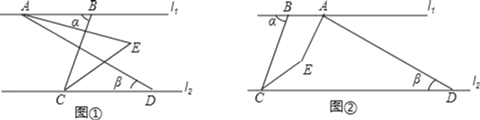
（1）如图①，求∠AEC的度数；
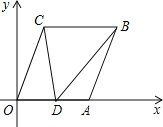
（2）如图②，将线段AD沿CD方向平移，其他条件不变，求∠AEC的度数．
【答案】（1）∠AEC＝50°；（2）∠AEC＝140°．
【解析】
（1）利用平行线的性质结合角平分线的性质得出∠ECD以及∠AEF的度数即可得出答案；
（2）利用平行线的性质结合角平分线的性质得出∠BAE以及∠AEF的度数即可得出答案．
（1）过点E作EF∥l1，
∵l1∥l2，
∴EF∥l2，
∵l1∥l2，
∴∠BCD＝∠α，
∵∠α＝70°，
∴∠BCD＝70°，
∵CE是∠BCD的角平分线，
∴∠ECD＝
70°＝35°，
∵EF∥l2，
∴∠FEC＝∠ECD＝35°，
同理可求∠AEF＝15°，
∴∠AEC＝∠AEF+∠CEF＝50°；
（2）过点E作EF∥l1，
∵l1∥l2，
∴EF∥l2，
∵l1∥l2，
∴∠BCD＝∠α，
∵∠α＝70°，
∴∠BCD＝70°，
∵CE是∠BCD的角平分线，
∴∠ECD70°＝35°，
∵EF∥l2，
∴∠FEC＝∠ECD＝35°，
∵l1∥l2，
∴∠BAD+∠β＝180°，
∵∠β＝30°，
∴∠BAD＝150°，
∵AE平分∠BAD，
∴∠BAE＝150°＝75°，
∵EF∥l1，
∴∠BAE+∠AEF＝180°，
∴∠AEF＝105°，
∴∠AEC＝105°+35°＝140°．
阅读快车系列答案
【题目】把弹簧的上端固定，在其下端挂物体，下表是测得的弹簧长度
与所挂物体的质量
的一组对应值：
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 15 | 15．5 | 16 | 16．5 | 17 | 17．5 | … |
（1）表中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）弹簧的原长是_______
，物体每增加
，弹簧的长度增加_________．
（3）请你估测一下当所挂物体为
时，弹簧的长度是______．
