题目内容
（2007•崇安区一模）如图，已知抛物线y=
x2+mx+n（n≠0）与直线y=x交于A、B两点，与y轴交于点C，OA=OB，BC∥x轴．（1）求抛物线的解析式；
（2）设D、E是线段AB上异于A、B的两个动点（点E在点D的上方），DE=
，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．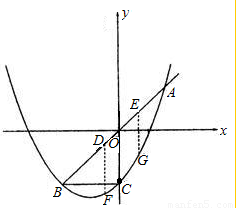
【答案】分析：（1）根据函数图象上点的坐标特点和函数图象交点与函数解析式组成的方程组的解之间的关系，求出B点坐标，再根据正比例函数图象上点的中心对称性，求出A点坐标，用待定系数法求解即可．
（2）根据各点坐标求出表示线段长的解析式，因为DF∥EG，可将四边形DEGF作为梯形来对待求其面积．
解答：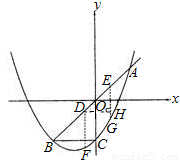
解：（1）∵抛物线y=
x2+mx+n与y轴交于点C
∴C（0，n）
∵BC∥x轴
∴B点的纵坐标为n
∵B、A在y=x上，且OA=OB
∴A（-n，-n），B（n，n）
∴
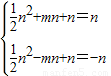
解得：n=0（舍去），n=-2；m=1
∴所求解析式为：y=
x2+x-2
（2）作DH⊥EG于H
∵D、E在直线y=x上
∴∠EDH=45°
∴DH=EH
∵DE=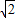
∴DH=EH=1
∵D（x，x）
∴E（1+x，1+x）
∴F的纵坐标：
x2+x-2，
G的纵坐标：
（x+1）2+（x+1）-2
∴DF=x-（
x2+x-2）=2-
x2，EG=（x+1）-[
（x+1）2+（x+1）-2]=2-
（x+1）2
∴y=
[2-
x2+2-
（x+1）2]×1
y=-
x2-
x+
，
y=-
（x+
）2+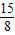
，
∴x的取值范围是-2＜x＜1．当x=-
时，y最大值=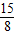
．
点评：此题是一道典型的数形结合性题目，通过坐标和函数解析式把面积问题转化为二次函数的最值问题是解答此题的关键．
（2）根据各点坐标求出表示线段长的解析式，因为DF∥EG，可将四边形DEGF作为梯形来对待求其面积．
解答：
解：（1）∵抛物线y=x2+mx+n与y轴交于点C∴C（0，n）
∵BC∥x轴
∴B点的纵坐标为n
∵B、A在y=x上，且OA=OB
∴A（-n，-n），B（n，n）
∴
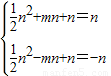
解得：n=0（舍去），n=-2；m=1
∴所求解析式为：y=
x2+x-2（2）作DH⊥EG于H
∵D、E在直线y=x上
∴∠EDH=45°
∴DH=EH
∵DE=
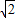
∴DH=EH=1
∵D（x，x）
∴E（1+x，1+x）
∴F的纵坐标：
x2+x-2，G的纵坐标：
（x+1）2+（x+1）-2∴DF=x-（
x2+x-2）=2-x2，EG=（x+1）-[（x+1）2+（x+1）-2]=2-（x+1）2∴y=
[2-x2+2-（x+1）2]×1y=-
x2-x+，y=-
（x+）2+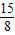，∴x的取值范围是-2＜x＜1．当x=-
时，y最大值=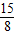．点评：此题是一道典型的数形结合性题目，通过坐标和函数解析式把面积问题转化为二次函数的最值问题是解答此题的关键．
练习册系列答案
相关题目