Question

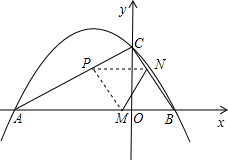
二次函数y=ax²+bx+c的图象如图所示，给出下列结论：
①2a+b＞0；②b＞a＞c；③若-1＜m＜n＜1，则m+n＜-；④3|a|+|c|＜2|b|．
其中正确的结论是    （写出你认为正确的所有结论序号）．

Answer 1

【答案】分析：分别根据二次函数开口方向以及对称轴位置和图象与y轴交点得出a，b，c的符号，再利用特殊值法分析得出各选项．
解答：解：∵抛物线开口向下，∴a＜0，∴2a＜0，
对称轴x=-＞1，-b＜2a，∴2a+b＞0，故选项①正确；
∵-b＜2a，∴b＞-2a＞0＞a，
令抛物线解析式为y=-x²+bx-，
此时a=c，欲使抛物线与x轴交点的横坐标分别为和2，
则=-，
解得：b=，
∴抛物线y=-x²+x-，符合“开口向下，与x轴的一个交点的横坐标在0与1之间，
对称轴在直线x=1右侧”的特点，而此时a=c，（其实a＞c，a＜c，a=c都有可能），
故②选项错误；
∵-1＜m＜n＜1，-2＜m+n＜2，
∴抛物线对称轴为：x=-＞1，＞2，m+n，故选项③正确；
当x=1时，a+b+c＞0，2a+b＞0，3a+2b+c＞0，
∴3a+c＞-2b，∴-3a-c＜2b，
∵a＜0，b＞0，c＜0，
∴3|a|+|c|=-3a-c＜2b=2|b|，故④选项正确．
故答案为：①③④．
点评：此题主要考查了二次函数图象与系数的关系，利用特殊值法求出m+n的取值范围是解题关键．