题目内容
 直线DE过点A,DE∥BC,∠B+∠C=120°,AF平分∠BAD,AG平分∠CAE,求∠FAG的度数.
直线DE过点A,DE∥BC,∠B+∠C=120°,AF平分∠BAD,AG平分∠CAE,求∠FAG的度数.
分析:根据题意可得出∠BAD+∠CAE=∠B+∠C=120°,再根据AF平分∠BAD,AG平分∠CAE,可得∠FAB+∠GAC的度数,继而可求得∠FAG的度数.
解答:解:∵DE∥BC(已知),
∴∠BAD=∠B,∠CAE=∠C(两直线平行,内错角相等),
∴∠BAD+∠CAE=∠B+∠C=120°,
∵AF平分∠BAD,AG平分∠CAE,(已知),
∴∠FAD=
∠BAD,∠GAE=
∠CAE(角平分线定义),
∴∠FAD+∠GAE=
(∠BAD+∠CAE)=60°,
∴∠FAG=180°-(∠FAD+∠GAE)=120°.
∴∠BAD=∠B,∠CAE=∠C(两直线平行,内错角相等),
∴∠BAD+∠CAE=∠B+∠C=120°,
∵AF平分∠BAD,AG平分∠CAE,(已知),
∴∠FAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FAD+∠GAE=
| 1 |
| 2 |
∴∠FAG=180°-(∠FAD+∠GAE)=120°.
点评:本题考查角平分线及平行线的性质,难度不算大,关键在于根据图形找出各角的关系.

练习册系列答案
相关题目
 22、如图,在Rt△ABC中,∠CAB=90°,AB=AC,直线DE过点A,CD⊥DE,BE⊥DE,CD=4,BE=3,求DE的长.
22、如图,在Rt△ABC中,∠CAB=90°,AB=AC,直线DE过点A,CD⊥DE,BE⊥DE,CD=4,BE=3,求DE的长.
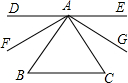 直线DE过点A,DE∥BC,∠B+∠C=120°,AF平分∠BAD,AG平分∠CAE,求∠FAG的度数.
直线DE过点A,DE∥BC,∠B+∠C=120°,AF平分∠BAD,AG平分∠CAE,求∠FAG的度数.