题目内容

设M1、M2是△ABC的BC边上的点，且BM1=CM2．任作一直线分别交AB、AC、AM1、AM2于P、Q、N1、N2．试证：
AB
AP
+
AC
AQ
=
AM1
AN1
+
AM2
AN2
．
分析：可过点A作PQ的平行线交直线BC于E．根据平行线分线段成比例定理以及比例的性质进行变形即可证明
AB
AP
+
AC
AQ
=
AM1
AN1
+
AM2
AN2
．
解答：证明：如图，若PQ∥BC，易证结论成立．
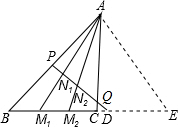
精英家教网
若PQ与BC不平行，
设PQ交直线BC于D．过点A作PQ的平行线交直线BC于E．
由BM1=CM2，可知BE+CE=M1E+M2E，
易知
AB
AP
=
BE
DE
，
AC
AQ
=
CE
DE
，
AM1
AN1
=
M1E
DE
，
AM2
AN2
=
M2E
DE
．
则
AB
AP
+
AC
AQ
=
BE+CE
DE
=
M1E+M2E
DE
=
AM1
AN1
+
AM2
AN2
．
所以，
AB
AP
+
AC
AQ
=
AM1
AN1
+
AM2
AN2
．
点评：本题主要考查了平行线分线段成比例定理，解题关键是添加一条平行线，将求证式中的四个线段比“通分”，使公分母为DE，于是问题迎刃而解．
练习册系列答案
相关题目
阅读下面材料，并解答下列各题：
在形如ab=N的式子中，我们已经研究过两种情况：
①已知a和b，求N，这是乘方运算；
②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记着b=logaN．
例如：因为23=8，所以log28=3；因为2-3=
1
8
，所以log2
1
8
=-3．
（1）根据定义计算：
①log381=
 
；②log33=
 
；③log31=
 
；
④如果logx16=4，那么x=
 
．
（2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，
即logaMN=logaM+logaN
这是对数运算的重要性质之一，进一步，我们还可以得出：
logaM1M2M3…Mn=
 
（其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）
loga
M
N
=
 
（a＞0，a≠1，M、N均为正数）．
在形如ab=N的式子中，我们已经研究过两种情况：
①已知a和b，求N，这是乘方运算；
②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作b=logaN．
例如：求log28，因为23=8，所以log28=3；又比如∵2-3=
1
8
，∴log2
1
8
=-3．
（1）根据定义计算：
①log381=
 
；②log101=
 
；③如果logx16=4，那么x=
 
．
（2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，即logaMN=logaM+logaN
这是对数运算的重要性质之一，进一步，我们还可以得出：logaM1M2M3…Mn=
 
．
（其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）．
（3）请你猜想：loga
M
N
=
 
（a＞0，a≠1，M、N均为正数）．
（2001•泰州）在形如ab=N的式子中，我们已经研究过两种情况：
①已知a和b，求N，这是乘方运算；
②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作b=logaN．
例如：求log28，因为23=8，所以log28=3；又比如∵，∴．
（1）根据定义计算：
①log381=______；②log101=______；③如果logx16=4，那么x=______．
（2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，即logaMN=logaM+logaN
这是对数运算的重要性质之一，进一步，我们还可以得出：logaM1M2M3…Mn=______．
（其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）．
（3）请你猜想：=______（a＞0，a≠1，M、N均为正数）．
（2001•泰州）在形如ab=N的式子中，我们已经研究过两种情况：
①已知a和b，求N，这是乘方运算；
②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作b=logaN．
例如：求log28，因为23=8，所以log28=3；又比如∵，∴．
（1）根据定义计算：
①log381=______；②log101=______；③如果logx16=4，那么x=______．
（2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，即logaMN=logaM+logaN
这是对数运算的重要性质之一，进一步，我们还可以得出：logaM1M2M3…Mn=______．
（其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）．
（3）请你猜想：=______（a＞0，a≠1，M、N均为正数）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网