题目内容
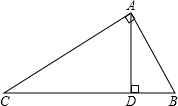 在△ABC中,∠C=90°,∠B=2∠A,CD⊥AB于D,若AB=10cm,则BD=________cm.
在△ABC中,∠C=90°,∠B=2∠A,CD⊥AB于D,若AB=10cm,则BD=________cm.
2.5
分析:由题意可得出∠BCD=∠A,又∠CDB=∠ACB=90°,所以△ACB∽△CDB,即: =
=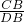 ,AB=
,AB=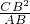 ,求出CB的值即可,在Rt△ABC,由∠A的正弦函数可得:BC=sin∠A×AB=5cm,代入求值.
,求出CB的值即可,在Rt△ABC,由∠A的正弦函数可得:BC=sin∠A×AB=5cm,代入求值.
解答:在△ABC中,∠C=90°,∠B=2∠A,
所以,∠A=30°,∠B=60°,BC=sin∠A×AB= ×10=5cm;
×10=5cm;
∵CD⊥AB
∴∠B+∠BCD=∠A+∠B=90°
即:∠BCD=∠A
又∵∠CDB=∠ACB=90°
∴△ACB∽△CDB
∴ =
=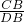
即:DB=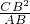 =
=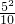 =2.5cm.
=2.5cm.
点评:本题主要考查相似三角形的判定定理与性质,关键在于找出条件判定两个三角形相似,再根据相似的性质求解.
分析:由题意可得出∠BCD=∠A,又∠CDB=∠ACB=90°,所以△ACB∽△CDB,即:
 =
=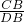 ,AB=
,AB=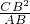 ,求出CB的值即可,在Rt△ABC,由∠A的正弦函数可得:BC=sin∠A×AB=5cm,代入求值.
,求出CB的值即可,在Rt△ABC,由∠A的正弦函数可得:BC=sin∠A×AB=5cm,代入求值.解答:在△ABC中,∠C=90°,∠B=2∠A,
所以,∠A=30°,∠B=60°,BC=sin∠A×AB=
 ×10=5cm;
×10=5cm;∵CD⊥AB
∴∠B+∠BCD=∠A+∠B=90°
即:∠BCD=∠A
又∵∠CDB=∠ACB=90°
∴△ACB∽△CDB
∴
 =
=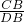
即:DB=
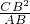 =
=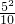 =2.5cm.
=2.5cm.点评:本题主要考查相似三角形的判定定理与性质,关键在于找出条件判定两个三角形相似,再根据相似的性质求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于