题目内容
等腰三角形的腰和底边的长分别为4和2，则腰上的高为________．
分析：作底边上的高，则底边上的高，腰长，底边的一半构成直角三角形，利用勾股定理即可求出底边上的高，设腰上的高为h，再根据2S△ABC=BC•AD=AB•h，代入数据计算即可．
解答：
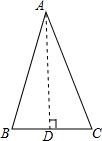解：如图，作底边上的高AD，则BD=
BC=1，根据勾股定理AD=
=
=
，设腰上的高为h，则
2S△ABC=4h=2×
，解得h=
．故腰上的高为
．点评：本题主要利用等腰三角形“三线合一”的性质和勾股定理求解．
练习册系列答案
相关题目