题目内容
已知过点(1,0)的直线与抛物线y=2x2仅有一个交点,写出满足该条件的直线解析式________.
y=8x-8或x=1或y=0
分析:设过点(1,0)的直线为y=kx+b,把(1,0)代入其中得k+b=0,又直线与抛物线y=2x2只有一个交点,那么它们组成的方程组只有一个实数解,那么关于x的方程的判别式为0,由此即可求出k和b.
解答:设过点(1,0)的直线为y=kx+b,
把(1,0)代入其中得k+b=0,
∴b=-k ①,
∴y=kx-k,
∵过点(1,0)的直线与抛物线y=2x2仅有一个交点,
∴kx-k=2x2的判别式为0,
即△=b2-4ac=k2-8k=0,∴k=8或k=0(不合题意,舍去),
∴当k=8时,b=-8,
当k=0时,b=0,
∴直线解析式为y=8x-8或x=1或y=0.
故填空答案:y=8x-8或x=1或y=0.
点评:此题主要考查了抛物线与直线的交点情况与它们解析式组成的方程组的解之间的关系,解题根据是利用它们之间的对应关系列出关于待定系数的方程.
分析:设过点(1,0)的直线为y=kx+b,把(1,0)代入其中得k+b=0,又直线与抛物线y=2x2只有一个交点,那么它们组成的方程组只有一个实数解,那么关于x的方程的判别式为0,由此即可求出k和b.
解答:设过点(1,0)的直线为y=kx+b,
把(1,0)代入其中得k+b=0,
∴b=-k ①,
∴y=kx-k,
∵过点(1,0)的直线与抛物线y=2x2仅有一个交点,
∴kx-k=2x2的判别式为0,
即△=b2-4ac=k2-8k=0,∴k=8或k=0(不合题意,舍去),
∴当k=8时,b=-8,
当k=0时,b=0,
∴直线解析式为y=8x-8或x=1或y=0.
故填空答案:y=8x-8或x=1或y=0.
点评:此题主要考查了抛物线与直线的交点情况与它们解析式组成的方程组的解之间的关系,解题根据是利用它们之间的对应关系列出关于待定系数的方程.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
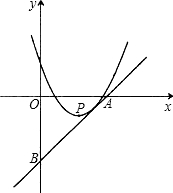 如图,已知过点(
如图,已知过点(