Question

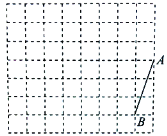
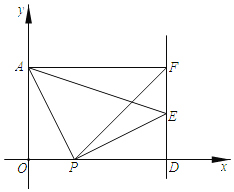
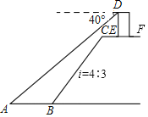
【题目】如图，这是某水库大坝截面示意图，张强在水库大坝顶CF上的瞭望台D处，测得水面上的小船A的俯角为40°，若DE＝3米，CE＝2米，CF平行于水面AB，瞭望台DE垂直于坝顶CF，迎水坡BC的坡度i＝4：3，坡长BC＝10米，求小船A距坡底B处的长．（结果保留0.1米）（参考数据：sin40°≈0.64，cos40°＝0.77，tan40°≈0.84）

Answer 1

【答案】AB的长约为5.1米．

【解析】

延长DE交AB延长线于点P，作于点Q，构造Rt△ADP和Rt△BCQ.利用坡度表示出CQ，BQ的长，进而求出DP长，在Rt△ADP，即可求出AP，由AB=AP-BQ-PQ即可得到答案.

解：如图，延长DE交AB延长线于点P，作于点Q，

∵，，∴．

∴四边形CEPQ为矩形．

∴，

∵，

∴设，．

在中，由勾股定理，得，即．

解得或（舍）．

∴，．

∴．

在中，∵

∴．

∴（米）．

答：AB的长约为5.1米．