题目内容
【题目】如图,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,若
上,若![]() ,
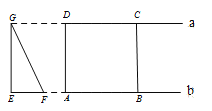
,![]() 从如图所示的位置出发,沿直线
从如图所示的位置出发,沿直线![]() 向右匀速运动,直到
向右匀速运动,直到![]() 与
与![]() 重合.运动过程中
重合.运动过程中![]() 与矩形
与矩形![]() 重合部分的面积
重合部分的面积![]() 随时间
随时间![]() 变化的图象大致是( )
变化的图象大致是( )
A. 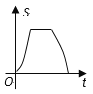 B.
B. 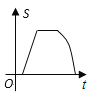 C.
C. 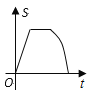 D.
D. 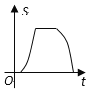
【答案】D
【解析】
理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.
根据题意可得:
①F、A重合之前没有重叠面积,
②F、A重叠之后到E与A重叠前,设AE=a,EF被重叠部分的长度为(t-a),则重叠部分面积为S=![]() (t-a)(t-a)tan∠EFG=
(t-a)(t-a)tan∠EFG=![]() (t-a)2tan∠EFG,
(t-a)2tan∠EFG,
∴是二次函数图象;
③△EFG完全进入且F与B重合之前,重叠部分的面积是三角形的面积,不变,
④F与B重合之后,重叠部分的面积等于S=S△EFG-![]() (t-a)2tan∠EFG,符合二次函数图象,直至最后重叠部分的面积为0.
(t-a)2tan∠EFG,符合二次函数图象,直至最后重叠部分的面积为0.
综上所述,只有D选项图形符合.
故选D.

练习册系列答案
相关题目