题目内容
梯形ABCD中,AD∥BC,∠A=90°,AC⊥BD,AD=1,BC=4,则两条对角线AC:BD为
- A.4:1
- B.2:1
- C.
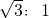
- D.2:

B
分析:过A作AE∥BD,根据平形四边形的性质得到△AEB∽△CAB,利用相似三角形的性质求得AB的长,然后利用△AEC∽△ABC求得结论即可.
解答: 过A作AE∥BD
过A作AE∥BD
∵AE∥BD,AD∥BC
∴AEBD为平行四边形
∴AE=BD,AD=BE
∵AC⊥BD
∴AE⊥AC
∵∠A=90°
∴AB⊥BC
∴∠ACB+∠AEB=∠AEB+∠EAB=90°
∴∠ACB=∠EAB
∴△AEB∽△CAB
∴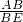 =
=
∴AB2=BC×BE=1×4=4
∴AB=2
∵AB⊥BC,AE⊥AC
∴△AEC∽△ABC
∴ =
= =
= =
=
∴AC:BD=2:1
故选B.
点评:本题考查了相似三角形的性质,解题的过程中两次用到了相似三角形,难度较大.
分析:过A作AE∥BD,根据平形四边形的性质得到△AEB∽△CAB,利用相似三角形的性质求得AB的长,然后利用△AEC∽△ABC求得结论即可.
解答:
 过A作AE∥BD
过A作AE∥BD∵AE∥BD,AD∥BC
∴AEBD为平行四边形
∴AE=BD,AD=BE
∵AC⊥BD
∴AE⊥AC
∵∠A=90°
∴AB⊥BC
∴∠ACB+∠AEB=∠AEB+∠EAB=90°
∴∠ACB=∠EAB
∴△AEB∽△CAB
∴
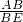 =
=
∴AB2=BC×BE=1×4=4
∴AB=2
∵AB⊥BC,AE⊥AC
∴△AEC∽△ABC
∴
 =
= =
= =
=
∴AC:BD=2:1
故选B.
点评:本题考查了相似三角形的性质,解题的过程中两次用到了相似三角形,难度较大.

练习册系列答案
相关题目
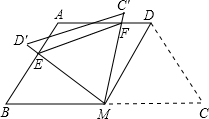 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点. DE.
DE. 如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.
如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.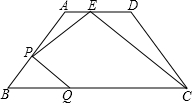 如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是
如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是 分别交边CD、BC于点F、E,若AD=3,BC=12,
分别交边CD、BC于点F、E,若AD=3,BC=12,