题目内容
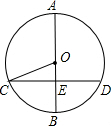（2012•珠海）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=26，CD=24，那么sin∠OCE=| 5 |
| 13 |
| 5 |
| 13 |
分析：根据果AB=26，判断出半径OC=13，再根据垂径定理求出CE=
CD=12，在Rt△OCE中，利用勾股定理求出OE的长，再根据正弦函数的定义，求出sin∠OCE的度数．
| 1 |
| 2 |
解答：解：如图：
∵AB为⊙0直径，AB=26，
∴OC=
×26=13，
又∵CD⊥AB，
∴CE=
CD=12，
在Rt△OCE中，OE=
=
=5，
∴sin∠OCE=
=
．
故答案为
．
∵AB为⊙0直径，AB=26，
∴OC=
| 1 |
| 2 |
又∵CD⊥AB，
∴CE=
| 1 |
| 2 |
在Rt△OCE中，OE=
| OC2-CE2 |
| 132-122 |
∴sin∠OCE=
| OE |
| OC |
| 5 |
| 13 |
故答案为
| 5 |
| 13 |
点评：本题考查了垂径定理、勾股定理、锐角三角形的定义，旨在考查同学们的应用能力．
练习册系列答案
学习实践园地系列答案
相关题目
（2012•珠海）如图，二次函数y=（x-2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．
（2012•珠海）如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．
（2012•珠海）如图，水渠边有一棵大木瓜树，树干DO（不计粗细）上有两个木瓜A、B（不计大小），树干垂直于地面，量得AB=2米，在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°．求C处到树干DO的距离CO．（结果精确到1米）（参考数据：
（2012•珠海）如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．
（2012•珠海）如图，在等腰梯形ABCD中，AB∥DC，AB=