题目内容
【题目】平面内的两条直线有相交和平行两种位置关系.
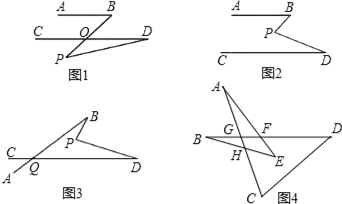
(1)如图1,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D.得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在如图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明);
(3)根据(2)的结论求如图4中∠A+∠B+∠C+∠D+∠E的度数.
【答案】(1)不成立,结论是∠BPD=∠B+∠D(2)结论:∠BPD=∠BQD+∠B+∠D(3)∠A+∠B+∠C+∠D+∠E=180°
【解析】(1)不成立,结论是∠BPD=∠B+∠D.
延长BP交CD于点E,
∵AB∥CD,∴∠B=∠BED,
又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D;
(2)结论:∠BPD=∠BQD+∠B+∠D.
连接QP并延长,
∵∠BPE是△BPQ的外角,∠DPE是△PDQ的外角,
∴∠BPE=∠B+∠BQE,∠DPE=∠D+∠DQP,
∴∠BPE+∠DPE=∠B+∠D+∠BQE+∠DQP,即∠BPD=∠BQD+∠B+∠D;
(3)由(2)的结论得:∠AFG=∠B+∠E.∠AGF=∠C+∠D.
又∵∠A+∠AFG+∠AGF=180°
∴∠A+∠B+∠C+∠D+∠E=180°.
(或由(2)的结论得:∠AGB=∠A+∠B+∠E且∠AGB=∠CGD,
∴∠A+∠B+∠C+∠D+∠E=180°.



【题目】观察月历.
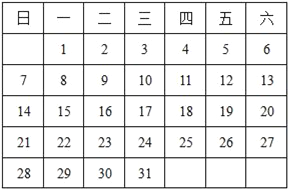
(1)根据月历中的规律填空:
| a |
|
|
(2)莉莉国庆假期外出旅行三天,三天日期之和是27,莉莉是 号出发的.
(3)某月小林连续三周周六外出参加羽毛球比赛并获得冠军,三天日期之和是51.
①小林是 号夺冠的.
②本月1号星期 .