题目内容
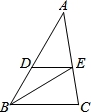
如图,△ABC中,点D、E分别在AB、AC上,且DE∥BC,若S△ADE=4,S△BDE=3,那么DE:BC=__________.
4:7.
【考点】相似三角形的判定与性质.
【分析】根据 =
= =
= ,得到
,得到 =
= ,通过△ADE∽△ABC,根据相似三角形的性质得到DE:BC=AD:AB=4:7.
,通过△ADE∽△ABC,根据相似三角形的性质得到DE:BC=AD:AB=4:7.
【解答】解:∵S△ADE=4,S△BDE=3,
∴ =
= =
= ,
,
∴ =
= ,
,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AD:AB=4:7.
故答案为:4:7.
【点评】本题考查了相似三角形的判定和性质,知道不等底同高的三角形的面积比等于底的比是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
|﹣3|结果为( )
| A. ﹣3 | B. 3 | C. | D. ﹣ |
下列交通标志中,既是轴对称图形又是中心对称图形的是
|
|
|
|
| |
| A | B | C | D |

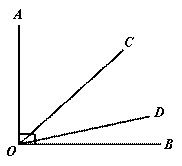 与OA成180°时,OC与OD同时停止旋转.
与OA成180°时,OC与OD同时停止旋转. .
.




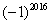 结果正确的是
结果正确的是