Question

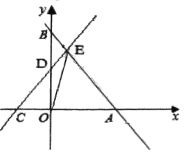
【题目】如图，在平面直角坐标系中，直线与轴、轴分别交于点，直线与轴、轴分别交于点，，的解析式为，的解析式为且，两直线的交点。

（1）求直线的解析式；

（2）求四边形的面积；

（3）当时，直接写出的取值范围。

Answer 1

【答案】（1）；（2）108；（3）x<3

【解析】

（1）分别求出点A,B,E的坐标，利用求出点C的坐标，然后利用待定系数法求直线CD的解析式；（2）求出点D坐标，然后利用四边形等于△DOE与△AOE的面积之和，即可求解；（3）结合图像，根据点E的坐标确定不等式的解集.

解：（1）在中

当x=0时，y=16

当y=0时，

解得：

∴点A(12,0)；点B(0,16)

将点代入中

∴点

又∵

∴点C(-6,0)

将点C,E代入直线CD的解析式为得：

解得：

∴直线CD的解析式为

（2）在中

当x=0时，y=8

∴点D的坐标为（0，8）

∴四边形的面积=S△DOE+S△AOE

∴

（3）∵两直线的交点

∴结合图像可得，的解集为：x<3