Question

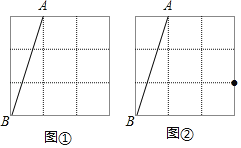
【题目】如图，在每个小正方形边长为的网格中，的顶点，，均在格点上，为边上的一点.

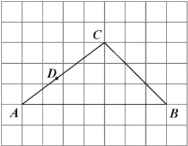
（Ⅰ）线段的值为______________;

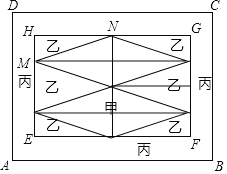
（Ⅱ）在如图所示的网格中，是的角平分线，在上求一点，使的值最小，请用无刻度的直尺，画出和点，并简要说明和点的位置是如何找到的（不要求证明）___________.

Answer 1

【答案】（Ⅰ） （Ⅱ）如图，取格点、，连接与交于点，连接与交于点.

【解析】

（Ⅰ）根据勾股定理进行计算即可.

（Ⅱ）根据菱形的每一条对角线平分每一组对角，构造边长为5的菱形ABEC，连接AE交BC于M，即可得出是的角平分线，再取点F使AF=5，则根据等腰三角形的性质得出点C与F关于AM对称，连接DF交AM于点P，此时的值最小．

（Ⅰ）根据勾股定理得AC=；

故答案为：5．

（Ⅱ）如图，如图，取格点、，连接与交于点，连接与交于点，则点P即为所求．

说明：构造边长为5的菱形ABEC，连接AE交BC于M，则AM即为所求的的角平分线，在AB上取点F，使AF=AC=5，则AM垂直平分CF，点C与F关于AM对称，连接DF交AM于点P，则点P即为所求．