��Ŀ����
����Ŀ����ͼ����Rt��ABC�Ķ���A��B��x���ϣ���C��y�����������ϣ���
A(��1��0)��B(4��0)����ACB��90��.
(1)���A��B��C����������߽���ʽ��
(2)�������ߵĶԳ���l��BC�߽��ڵ�D����P�ǶԳ���l�ϵĵ㣬��������P��C��DΪ��������������AOC���ƣ���P������ꣻ
(3)�ڶԳ���l�����������Ƿ�ֱ���ڵ�M��N��ʹ����A��O��M��NΪ������ı�����ƽ���ı��Σ���������ֱ��д����M����N�����ꣻ�������ڣ���˵������.
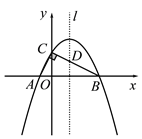
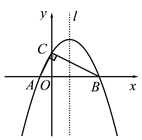
ͼ1 ����ͼ
���𰸡�������
��������������(1)����![]() �����
�����![]() �����꣬�ô���ϵ����������������ߵĽ���ʽ.
�����꣬�ô���ϵ����������������ߵĽ���ʽ.
(2)����������������ۼ���.
(3)����. ����ֱ��l�ϴ��ڵ�M���������ϴ��ڵ�N��ʹ����A��O��M��NΪ������ı���Ϊƽ���ı���.�ֵ�ƽ���ı���![]() ��ƽ���ı���ʱ����ƽ���ı���AONM��ƽ���ı���ʱ�����ı���AMONΪƽ���ı���ʱ�����������������.
��ƽ���ı���ʱ����ƽ���ı���AONM��ƽ���ı���ʱ�����ı���AMONΪƽ���ı���ʱ�����������������.
��⣺(1)��֤![]() ����
����![]() ��
��![]()
��OC=2����C(0��2),
�������߹���A(-1��0)��B(4��0)
��˿��������ߵĽ���ʽΪ![]()
��C��(0��2)�����:![]() ����
����![]()
�������ߵĽ���ʽΪ![]()
(2)��ͼ2��
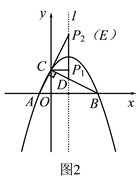
��![]() ʱ��
ʱ��![]() ��P1(
��P1(![]() ��2),
��2),
��![]() ʱ��
ʱ��![]()
��OC��l,
��![]() ��
��
��P2H��![]() ��OC��5��
��OC��5��
��P2 (![]() ��5)
��5)
���P�������Ϊ(![]() ��2)��(
��2)��(![]() ��5).
��5).
(3)����.
����ֱ��l�ϴ��ڵ�M���������ϴ��ڵ�N��ʹ����A��O��M��NΪ������ı���Ϊƽ���ı���.
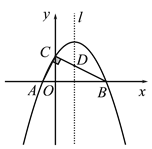
��ͼ3��

��ƽ���ı���![]() ��ƽ���ı���ʱ��M(
��ƽ���ı���ʱ��M(![]() ��
��![]() )��
)��![]() (
(![]() ,
,![]() ),
),
��ƽ���ı���AONM��ƽ���ı���ʱ��M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() ),
),
��ͼ4�����ı���AMONΪƽ���ı���ʱ��MN��OA����ƽ�֣���ʱ����M(![]() ��m)����
��m)���� ![]()

����N��������![]() �ϣ�
�ϣ�
��-m��-![]() ��(-
��(-![]() +1)( -
+1)( -![]() -4)=-
-4)=-![]() ,
,
��m=![]() ,
,
��ʱM(![]() ��
��![]() )�� N(-
)�� N(-![]() ,-
,-![]() ).
).
����������M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() )��M(
)��M(![]() ��
��![]() )��N(
)��N(![]() ,
,![]() ) �� M(
) �� M(![]() ��
��![]() )�� N(-
)�� N(-![]() ,-
,-![]() ).
).

 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�



