题目内容

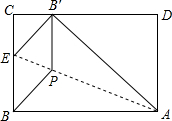
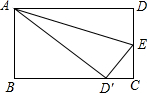
如图，矩形ABCD纸片的长为2a，宽为a，将纸片ABCD折叠，使点D落在BC的中点E处，点A落在F处，折痕为MN，则线段CN的长是______．
设CN=x，则DN=（2a-x），由折叠的性质知EN=DN=（2a-x），而EC=
1
2
a，
在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（2a-x）2=
1
4
a2+x2，
整理得4ax=
15
4
a2，所以x=
15
16
a．
故答案为：
15
16
a．
练习册系列答案
相关题目
矩形纸片ABCD中，AB=5，AD=4，将纸片折叠，使点B落在边CD上的B′处，折痕为AE，点P是AE上的一点，且BP=BE，连接B′P．
（1）求B′D的长；
（2）求证：四边形BPB′E的形状为菱形；
（3）若在折痕AE上存在一点到边CD的距离与到点B的距离相等，请直接写出此相等距离的值．
如图，在△ABC中，D是BC的中点，E、F分别在AB、AC上且∠EDF=90°．
（1）画出点F关于直线ED对称的对称点F1；
（2）连结BF1和DF1，△BF1D与△CFD有怎样的位置关系？说明理由．
如图，矩形OABC的边OA、OC分别在x轴、y轴上，点D、E分别在AB、BC边上，BD=BE=1．沿直线DE将△BDE翻折，点B落在点B′处．若点B′的坐标为（3，2）．则矩形OABC的面积为（　　）
A．8B．9C．10D．12
将一张矩形纸片对折如下图所示．然后沿图③中的虚线剪下（满足AB=CB），得到甲、乙两个部分，将甲展开后得到的平面图形是______．
已知矩形纸片ABCD中，AB=4，BC=6．

（1）如图1，点E是BC边上的一点，BE=2，AE、BD交于点F．①求AF：FE的值；②求△BEF的面积；
（2）如图2，将矩形纸片沿MN折叠，使点B与边CD的中点重合，点A、B的对应点为A1、B1，A1B1与DN交于点G，求△MCB1和△B1DG的周长之比．
折叠长方形ABCD的一边AD，点D落在BC边的D′处，AE是折痕，已知AB=8cm，CD′=4cm，则AD的长为（　　）
A．6cmB．8cmC．10cmD．12cm
如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-2，3）、B（-3，2）、C（-1，1）．请在图中作出△ABC关于y轴对称的△A1B1C1（A、B、C的对应点分别是A1、B1、C1），并直接写出A1、B1、C1的坐标．
利用图形中的对称点，画出图形的对称轴．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网