题目内容
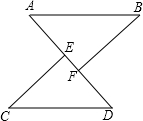如图所示，已知点A、E、F、D在同一条直线上，AE=DF，BF=CE，且BF∥CE
求证：△ABF≌△DCE．
证明：∵AE=DF，
∴AE+EF=DF+EF，
即AF=DE，
∵BF∥CE，
∴∠AFB=∠DEC，
在△ABF与△DCE中，
，
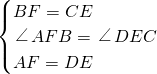∴△ABF≌△DCE．
分析：由AE=DF，可得出AF=DE，再由BF∥CE，得出∠AFB=∠DEC，即可证明△ABF≌△DCE．
点评：本题主要考查了全等三角形的判定，判定两个一般三角形全等的方法有四种：AAS，SAS，SSS，ASA．
∴AE+EF=DF+EF，
即AF=DE，
∵BF∥CE，
∴∠AFB=∠DEC，
在△ABF与△DCE中，
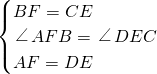，∴△ABF≌△DCE．
分析：由AE=DF，可得出AF=DE，再由BF∥CE，得出∠AFB=∠DEC，即可证明△ABF≌△DCE．
点评：本题主要考查了全等三角形的判定，判定两个一般三角形全等的方法有四种：AAS，SAS，SSS，ASA．
练习册系列答案
导学全程练创优训练系列答案
相关题目
如图所示，已知点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，FG=2，则CF的长为（ ）| A、4 | B、4.5 | C、5 | D、6 |
13、如图所示，已知点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，FG=2，则CF的长为
已知反比例函数y=
如图所示，已知点A（-3，4）和B（-2，1），试在y轴上求一点P，使PA+PB的值最小，并求出点P的坐标．