题目内容
 如图所示,抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3).
如图所示,抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3).
(1)求二次方程y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B,C两点距离之差最大?若存在,求出P点的坐标;若不存在,请说明理由.
解:(1)将C(0,-3)代入y=ax2+bx+c中,得到c=-3.
将c=-3,B(3,0)代入y=ax2+bx+c中,
得,9a+3b-3=0,
∴3a+b-1=0①
∵x=1是对称轴,
∴ ,
,
∵b=-2a,②
将②代入①的a=1,
∴b=-2,
∴二次函数的解析式是y=x2-2x-3.
(2)∵P在抛物线的对称轴上,又A、B是关于抛物线的对称轴对称,
∴PB=PA,即:|PB-PC|=|PA-PC|,
(根据对称性,求P到B和C的距离之差就是求P到A和C的距离之差)
∴P、C、A三点共线的时候这个差最大.
∵C点的坐标是(0,-3),A点的坐标是(-1,0),
∴直线AC的解析式是y=-3x-3;
又因为对称轴为x=1,
所以点P坐标是(1,-6).
分析:(1)将B、C的坐标代入抛物线的解析式中,联立抛物线的对称轴方程,即可求得该抛物线的解析式.
(2)由于A、B关于抛物线的对称轴对称,若P到B、C的距离差最大,那么P点必为直线AC与抛物线对称轴的交点,可先求出直线AC的解析式,联立抛物线对称轴方程,即可得到点P的坐标.
点评:此题主要考查了二次函数解析式的确定、轴对称的性质等重要知识点,难度适中;(2)题中能够正确的判断出点P的位置是解题的关键.
将c=-3,B(3,0)代入y=ax2+bx+c中,
得,9a+3b-3=0,
∴3a+b-1=0①
∵x=1是对称轴,
∴
 ,
,∵b=-2a,②
将②代入①的a=1,
∴b=-2,
∴二次函数的解析式是y=x2-2x-3.
(2)∵P在抛物线的对称轴上,又A、B是关于抛物线的对称轴对称,
∴PB=PA,即:|PB-PC|=|PA-PC|,
(根据对称性,求P到B和C的距离之差就是求P到A和C的距离之差)
∴P、C、A三点共线的时候这个差最大.
∵C点的坐标是(0,-3),A点的坐标是(-1,0),
∴直线AC的解析式是y=-3x-3;
又因为对称轴为x=1,
所以点P坐标是(1,-6).
分析:(1)将B、C的坐标代入抛物线的解析式中,联立抛物线的对称轴方程,即可求得该抛物线的解析式.
(2)由于A、B关于抛物线的对称轴对称,若P到B、C的距离差最大,那么P点必为直线AC与抛物线对称轴的交点,可先求出直线AC的解析式,联立抛物线对称轴方程,即可得到点P的坐标.
点评:此题主要考查了二次函数解析式的确定、轴对称的性质等重要知识点,难度适中;(2)题中能够正确的判断出点P的位置是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
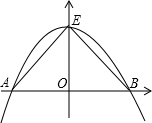 如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )
如图所示,抛物线y=ax2+bx+c与两坐标轴的交点分别是A、B、E,且△ABE是等腰直角三角形,AE=BE,则下列关系式中不能成立的是( )| A、b=0 | B、S△ABE=c2 | C、ac=-1 | D、a+c=0 |
 (2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(2012•河源二模)已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0). (2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).
(2012•槐荫区一模)如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).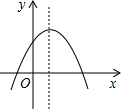 (1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( )
(1997•陕西)如图所示,抛物线对应的函数解析表达式只可能是( ) (1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;
(1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;