题目内容
如图,边长为4的等边△AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.在点P的运动过程中,线段BP的中点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.(1)当点P运动到线段OA的中点时,点C的坐标为______

【答案】分析:(1)过点作CD⊥x轴于点D,先由等边三角形的性质求出P点坐标及BP的长,故可得出PE的长,由图形旋转的性质求出PC=PE及∠CPD的度数,再由锐角三角函数的定义即可求出PD及CD的长,进而可得出结论;
(2)过P作PD⊥OB于点D,过C作CF⊥PA于点F,在Rt△OPD中 PD=OP•sin60°= ,由相似三角形的判定定理得出△BPD∽△PCF,故可得出CF及PF的长,进而可得出C点坐标;
,由相似三角形的判定定理得出△BPD∽△PCF,故可得出CF及PF的长,进而可得出C点坐标;
(3)取OA的中点M,连接MC,由(2)得 ,
, ,由锐角三角函数的定义得出∠CMF=30°,可知点C在直线MC上运动.故当点P在点O时,点C与点M重合.
,由锐角三角函数的定义得出∠CMF=30°,可知点C在直线MC上运动.故当点P在点O时,点C与点M重合.
当点P运动到点A时,点C的坐标为(5, ),由两点间的距离公式即可得出结论.
),由两点间的距离公式即可得出结论.
解答: 解:(1)如图1,过点作CD⊥x轴于点D,
解:(1)如图1,过点作CD⊥x轴于点D,
∵△AOB是等边三角形,P是OA的中点,
∴P(2,0),BP=OB•sin60°=4× =2
=2 ,
,
∵E是BP的中点,
∴PE= ,
,
∴PE=PC= ,
,
∵∠BPC=60°,
∴∠CPA=30°,
∴PD=PC•cos30°= ×
× =
= ,CD=PC•sin30°=
,CD=PC•sin30°= ×
× =
= ,
,
∴OD=OP+PD=2+ =
= ,
,
∴C( ,
, );
);
(2)如图2,过P作PD⊥OB于点D,过C作CF⊥PA于点F
在Rt△OPD中 PD=OP•sin60°= ,
,
∵∠OBP+∠OPB=∠CPF+∠OPB=120°
∴∠DBP=∠FPC,
∵∠PDB=∠CFP=90°
∴△BPD∽△PCF,
∴CF= ,
,
∴点C的坐标是( );
);

(3)取OA的中点M,连接MC,由(2)得 ,
, .
.
∴
∴∠CMF=30°.
∴点C在直线MC上运动.
当点P在点O时,点C与点M重合.
当点P运动到点A时,点C的坐标为
∴点C所经过的路径长为 .
.
点评:本题考查的是相似形综合题及旋转的性质、等边三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
(2)过P作PD⊥OB于点D,过C作CF⊥PA于点F,在Rt△OPD中 PD=OP•sin60°=
 ,由相似三角形的判定定理得出△BPD∽△PCF,故可得出CF及PF的长,进而可得出C点坐标;
,由相似三角形的判定定理得出△BPD∽△PCF,故可得出CF及PF的长,进而可得出C点坐标;(3)取OA的中点M,连接MC,由(2)得
 ,
, ,由锐角三角函数的定义得出∠CMF=30°,可知点C在直线MC上运动.故当点P在点O时,点C与点M重合.
,由锐角三角函数的定义得出∠CMF=30°,可知点C在直线MC上运动.故当点P在点O时,点C与点M重合.当点P运动到点A时,点C的坐标为(5,
 ),由两点间的距离公式即可得出结论.
),由两点间的距离公式即可得出结论.解答:
 解:(1)如图1,过点作CD⊥x轴于点D,
解:(1)如图1,过点作CD⊥x轴于点D,∵△AOB是等边三角形,P是OA的中点,
∴P(2,0),BP=OB•sin60°=4×
 =2
=2 ,
,∵E是BP的中点,
∴PE=
 ,
,∴PE=PC=
 ,
,∵∠BPC=60°,
∴∠CPA=30°,
∴PD=PC•cos30°=
 ×
× =
= ,CD=PC•sin30°=
,CD=PC•sin30°= ×
× =
= ,
,∴OD=OP+PD=2+
 =
= ,
,∴C(
 ,
, );
);(2)如图2,过P作PD⊥OB于点D,过C作CF⊥PA于点F

在Rt△OPD中 PD=OP•sin60°=
 ,
,∵∠OBP+∠OPB=∠CPF+∠OPB=120°
∴∠DBP=∠FPC,
∵∠PDB=∠CFP=90°
∴△BPD∽△PCF,
∴CF=
 ,
,
∴点C的坐标是(
 );
); 
(3)取OA的中点M,连接MC,由(2)得
 ,
, .
.∴

∴∠CMF=30°.
∴点C在直线MC上运动.
当点P在点O时,点C与点M重合.
当点P运动到点A时,点C的坐标为

∴点C所经过的路径长为
 .
.点评:本题考查的是相似形综合题及旋转的性质、等边三角形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
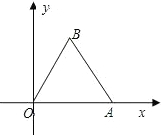 如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线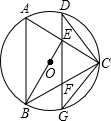 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
 (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长. (2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是
(2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是