题目内容
已知抛物线y=x2+bx+c交y轴于点A,点A关于抛物线对称轴的对称点为B(3,-4),直线y= x与抛物线在第一象限的交点为C,连接OB.
x与抛物线在第一象限的交点为C,连接OB.
(1)填空:b=______,c=______;
(2)如图(1),点P为射线OC上的动点,连接BP,设点P的横坐标为x,△OBP的面积为S,求S关于x的函数关系式;
(3)如图(2),点P在直线OC上的运动,点Q在抛物线上运动,问是否存在P、Q,使得以O,B,P,Q为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

解:(1)已知B(3,-4),根据抛物线的对称性可知A(0,-4),
将A、B两点坐标代入抛物线解析式,得
 ,解得b=-3,c=-4;
,解得b=-3,c=-4;
(2)作PD⊥y轴,则D(0, x)
x)
梯形ABPD面积= (x+3)(
(x+3)( x+4)=
x+4)= +
+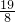 x+6
x+6
△AOB面积= ×3×4=6
×3×4=6
△DOP面积= ×x×
×x× x=
x=
∴S=梯形ABPD面积-△AOB面积-△DOP面积=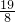 x
x
(3)存在.设P(4y,y),Q(x,x2-3x-4),
则OB=PQ,OQ=BP,
∵B(3,-4),
∴OB=5,
∴PB2=(4y-3)2+(y+4)2=x2+(x2-3x-4)2,①
OB2=(4y-x)2+(x2-3x-4-y)2=25,②
①②联立得, ,
, ,
, ,
, .
.
故P1(8,2),P2( ,
, ),P3(-
),P3(- ,-
,-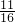 ),P4(
),P4( ,
,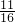 ).
).
分析:(1)根据B点坐标及抛物线的对称性,可求A点坐标,将A、B两点坐标代入抛物线解析式,解方程组可求b、c;
(2)连接AB,作PD⊥y轴,则D(0, x),在梯形ABPD中,分别计算梯形、两个直角三角形的面积,利用割补法表示△OBP的面积S;
x),在梯形ABPD中,分别计算梯形、两个直角三角形的面积,利用割补法表示△OBP的面积S;
(3)因为AB=3,根据PQ∥AB,PQ=AB,求出满足条件的P点坐标.
点评:本题考查了待定系数法求抛物线解析式的方法,坐标系中,面积的表示方法及平行四边形性质的运用.
将A、B两点坐标代入抛物线解析式,得
 ,解得b=-3,c=-4;
,解得b=-3,c=-4;
(2)作PD⊥y轴,则D(0,
 x)
x)梯形ABPD面积=
 (x+3)(
(x+3)( x+4)=
x+4)= +
+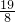 x+6
x+6△AOB面积=
 ×3×4=6
×3×4=6△DOP面积=
 ×x×
×x× x=
x=
∴S=梯形ABPD面积-△AOB面积-△DOP面积=
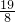 x
x(3)存在.设P(4y,y),Q(x,x2-3x-4),
则OB=PQ,OQ=BP,
∵B(3,-4),
∴OB=5,
∴PB2=(4y-3)2+(y+4)2=x2+(x2-3x-4)2,①
OB2=(4y-x)2+(x2-3x-4-y)2=25,②
①②联立得,
 ,
, ,
, ,
, .
.故P1(8,2),P2(
 ,
, ),P3(-
),P3(- ,-
,-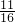 ),P4(
),P4( ,
,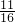 ).
).分析:(1)根据B点坐标及抛物线的对称性,可求A点坐标,将A、B两点坐标代入抛物线解析式,解方程组可求b、c;
(2)连接AB,作PD⊥y轴,则D(0,
 x),在梯形ABPD中,分别计算梯形、两个直角三角形的面积,利用割补法表示△OBP的面积S;
x),在梯形ABPD中,分别计算梯形、两个直角三角形的面积,利用割补法表示△OBP的面积S;(3)因为AB=3,根据PQ∥AB,PQ=AB,求出满足条件的P点坐标.
点评:本题考查了待定系数法求抛物线解析式的方法,坐标系中,面积的表示方法及平行四边形性质的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.