Question

如图，小明骑车从位于路灯P的北偏东60°方向与路灯P的距离为800米的A处出发，沿正南方向行进一段时间后，到达位于路灯P的南偏东45°方向上的B处．你能求此时小明所在的B处与路灯P的距离吗？（结果保留根号）．

Answer 1

解：作PC⊥AB于C点，
∴∠APC=30°，∠BPC=45° AP=800m．
在Rt△APC中，cos∠APC=，
∴PC=PA•cos∠APC=400（m）．
在Rt△PCB中，cos∠BPC=，
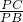∴PB===400（m）．
答：此时小明所在的B处与路灯P的距离是400m．
分析：过点P作PC⊥AB，则在Rt△APC中易得PC的长，再在直角△BPC中求出PB．
点评：此题主要考查了方向角问题，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．