题目内容
【题目】如图: 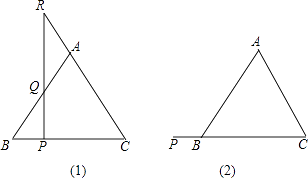
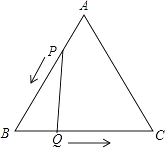
(1)P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
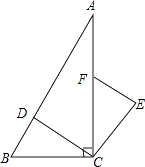
(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明.
【答案】
(1)解:AR=AQ,理由如下:
∵AB=AC,
∴∠B=∠C.
∵RP⊥BC,
∴∠B+∠BQP=∠C+∠PRC=90°,
∴∠BQP=∠PRC.
∵∠BQP=∠AQR,
∴∠PRC=∠AQR,
∴AR=AQ;
(2)解:猜想仍然成立.证明如下:

∵AB=AC,
∴∠ABC=∠C.
∵∠ABC=∠PBQ,
∴∠PBQ=∠C,
∵RP⊥BC,
∴∠PBQ+∠BQP=∠C+∠PRC=90°,
∴∠BQP=∠PRC,
∴AR=AQ
【解析】(1)由已知条件,根据等腰三角形两底角相等及三角形两直角互余的性质不难推出∠PRC与∠AQR的关系;(2)由已知条件,根据等腰三角形两底角相等及三角形两直角互余的性质不难推出∠BQP与∠PRC的关系.

练习册系列答案
相关题目