题目内容
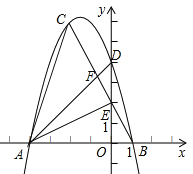
【题目】如图,已知抛物线![]() 经过点C(-2,6),
经过点C(-2,6),
与x轴相交于A、B两点(A在B的左侧),与y轴交于点D.
(1)求点A的坐标;
(2)设直线BC交y轴于点E,连接AE、AC,求证:![]() 是等腰直角三角形;
是等腰直角三角形;
(3)连接AD交BC于点F,试问当![]() 时,在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与
时,在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与![]() 相似?若存在, 请求出点P的坐标;若不存在,请说明理由.
相似?若存在, 请求出点P的坐标;若不存在,请说明理由.
【答案】(1)A(-4,0);(2)证明见解析;(3)存在,(-2,6)或![]() .
.
【解析】试题分析: (1)将点C(-2,6)代入解析式求出m的值,令y=0,求出A的坐标;
(2)根据两点间的距离公式求出AE、CE的长度,再根据股定理的逆定理判断出△AEC是等腰直角三角形;
(3)求出AD、BC的解析式组成方程组,解出F的坐标,根据三角形相似求出P点的坐标.
试题解析:

(1)∵抛物线![]() 经过点C(-2,6)
经过点C(-2,6)
∴![]()
∴![]()
∴![]()
∴当![]() ,
, ![]()
![]() ,
, ![]()
![]()
(2)证明:设直线BC的函数解析式为y=kx+b,
由题意得: ![]() ,解得:
,解得: ![]() .
.
∴直线BC的解析式为y=-2x+2.
∴点E的坐标为(0,2).
∴![]() .
.
∴AE=CE
又∵![]()
![]()
∴![]()
∴△AEC为等腰直角三角形
(3)在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与![]() 相似。理由如下:
相似。理由如下:

设直线AD的解析式为y=k1x+b1,则 ![]() ,解得:
,解得: ![]() .
.
∴直线AD的解析式为y=x+4。
联立直线AD与直线BC的函数解析式可得: ![]() ,解得:
,解得:  .
.
∴点F的坐标为(![]() ,
, ![]() )。
)。
则 ,
,
 。
。
又∵AB=5, ![]() ,
,
∴![]() .
.
∴![]() .
.
又∵∠ABF=∠CBA,∴△ABF∽△CBA。
∴当点P与点C重合时,以A、B、P为顶点的三角形与![]() 相似。
相似。
又∵抛物线关于直线![]() 对称
对称
当点P与点C的对称点重合时,以A、B、P为顶点的三角形也与![]() 相似。
相似。
∴当点P的坐标为(-2,6)或(-![]() 时,以A、B、P为顶点的三角形与
时,以A、B、P为顶点的三角形与![]() 相似。
相似。