题目内容
已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.
∵一次函数y=kx+b(k≠0)图象过点(0,2),
∴b=2,
令y=0,则x=-
,
∵函数图象与两坐标轴围成的三角形面积为2,
∴
×2×|-
|=2,即|-
|=2,
当k>0时,
=2,解得k=1;
当k<0时,-
=2,解得k=-1.
故此函数的解析式为:y=x+2或y=-x+2.
∴b=2,
令y=0,则x=-
| 2 |
| k |
∵函数图象与两坐标轴围成的三角形面积为2,
∴
| 1 |
| 2 |
| 2 |
| k |
| 2 |
| k |
当k>0时,
| 2 |
| k |
当k<0时,-
| 2 |
| k |
故此函数的解析式为:y=x+2或y=-x+2.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.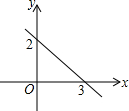 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.