题目内容
如图,⊙O是Rt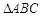 的外接圆,
的外接圆,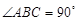 ,点P是圆外一点,PA切⊙O于点A,且PA = PB。求证:PB是⊙O的切线
,点P是圆外一点,PA切⊙O于点A,且PA = PB。求证:PB是⊙O的切线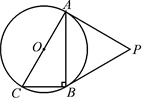
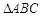 的外接圆,
的外接圆,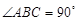 ,点P是圆外一点,PA切⊙O于点A,且PA = PB。求证:PB是⊙O的切线
,点P是圆外一点,PA切⊙O于点A,且PA = PB。求证:PB是⊙O的切线
证明:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO.
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB.
又∵OB是⊙O半径,
∴PB是⊙O的切线。
要证PB是⊙O的切线,只要连接OB,求证∠OBP=90°即可;

解答:
证明:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO.
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB.
又∵OB是⊙O半径,
∴PB是⊙O的切线。
说明:还可连接OB、OP,利用△OAP≌△OBP来证明OB⊥PB。

练习册系列答案
相关题目

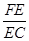 = .
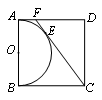
= .
 ,0)在以点A(1,0)为圆心,以2为半径的圆内, 则
,0)在以点A(1,0)为圆心,以2为半径的圆内, 则


 或
或
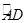 的中点,P是直径CD上一动点,则PA+PB的最小值为( )
的中点,P是直径CD上一动点,则PA+PB的最小值为( )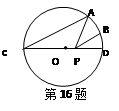
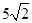
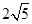
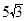



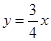 的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.
的图象上一点A(a,b),沿竖直方向向上移动6个单位,得到点B,再沿水平方向向右移动8个单位,得到点C.以AC为直径作圆E,设垂直于y轴的直线DT与圆E相切于点D.