题目内容
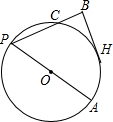如图，PA是⊙O的直径，PC是⊙O的弦，过AC弧的中点H作PC的垂线交PC的延长线于点B．若HB=6cm，BC=4cm，则⊙O的直径为（ ）A、2
| ||
B、3
| ||
| C、13cm | ||
D、6
|
分析：连接PH，OH，根据切线的判定可得到HB是圆的切线，再根据切割线定理及勾股定理求得BP，PH的长，利用相似三角形的判定方法得到Rt△BPH∽Rt△HPA，根据相似比即可求得直径的长．
解答：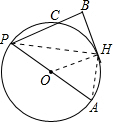
解：连接PH，OH，
∵H是
的中点，
∴∠HPC=∠APH，∠AOH=∠APC，
∴OH∥BC，
即OH⊥BH，
∴HB是⊙O的切线；
∵PB是⊙O的割线，HB=6cm，BC=4cm，
∴HB2=BC•BP，
∴36=4BP，
∴BP=9，
∴PH=
=
=
；
∵在Rt△BPH与Rt△HPA中，∠HPC=∠APH，
∴Rt△BPH∽Rt△HPA，
∴
=
，
∴AP=
=
=13cm；
故选C．
解：连接PH，OH，∵H是
 |
| AC |
∴∠HPC=∠APH，∠AOH=∠APC，
∴OH∥BC，
即OH⊥BH，
∴HB是⊙O的切线；
∵PB是⊙O的割线，HB=6cm，BC=4cm，
∴HB2=BC•BP，
∴36=4BP，
∴BP=9，
∴PH=
| BP2+BH2 |
| 92+62 |
| 117 |
∵在Rt△BPH与Rt△HPA中，∠HPC=∠APH，
∴Rt△BPH∽Rt△HPA，
∴
| BP |
| PH |
| PH |
| AP |
∴AP=
| PH2 |
| BP |
(
| ||
| 9 |
故选C．
点评：本题考查的是切线的判定定理，圆周角定理及切割线定理，解答此题的关键是作出辅助线，利用数形结合解答．
练习册系列答案
名校课堂系列答案
相关题目
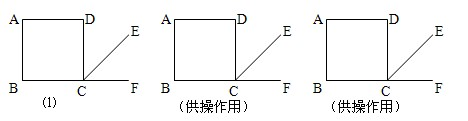
如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．
（如果需要，还可以继续操作、实验与测量）
1.操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．
|
| PA | PQ |
| 第一次 |
|
|
| 第二次 |
|
|
2.观测测量结果，猜测它们之间的关系：____________
3.请证明你猜测的结论；
4.当点P在BC的延长线上移动时，继续⑴的操作实验，试问：⑴中的猜测结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
（考查猜想、证明等综合能力）
如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．
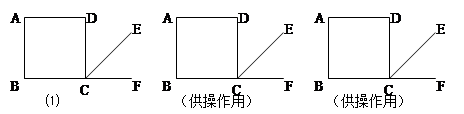
（如果需要，还可以继续操作、实验与测量）
【小题1】操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．
【小题2】观测测量结果，猜测它们之间的关系：____________
【小题3】请证明你猜测的结论；
【小题4】当点P在BC的延长线上移动时，继续⑴的操作实验，试问：⑴中的猜测结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
（考查猜想、证明等综合能力）
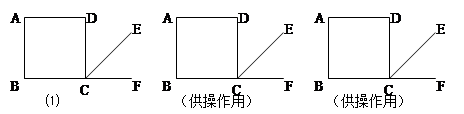
（如果需要，还可以继续操作、实验与测量）
【小题1】操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．
| | PA | PQ |
| 第一次 | | |
| 第二次 | | |
【小题2】观测测量结果，猜测它们之间的关系：____________
【小题3】请证明你猜测的结论；
【小题4】当点P在BC的延长线上移动时，继续⑴的操作实验，试问：⑴中的猜测结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
（考查猜想、证明等综合能力）
如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．
（如果需要，还可以继续操作、实验与测量）
1.操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．
|
|
PA |
PQ |
|
第一次 |
|
|
|
第二次 |
|
|
2.观测测量结果，猜测它们之间的关系：____________
3.请证明你猜测的结论；
4.当点P在BC的延长线上移动时，继续⑴的操作实验，试问：⑴中的猜测结论还成立吗？若成立，请给出证明；若不成立，请说明理由．
（考查猜想、证明等综合能力）