Question

已知∠AOB=90°，OM是∠AOB的平分线，将三角板的直角顶点P放在射线OM上滑动，两直角边分别与OA、OB交于C、D，PC和PD有怎样的数量关系，证明你的结论。

 

Answer 1

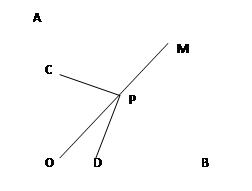
解：PC=PD

         证明：作PE⊥OA,PF⊥OB,垂足分别为E、F。

               则有 ∠EC=∠PFD=90°

               即 ∠PEO=∠PFD=90°

               ∵OM平分∠AOB

               ∴∠POE=∠POF

             于是 在△PEO和△PFO中

               

     ∵

                 ∴ △ PEO≌△PFO(AAS) ……………………6分

 

                  ∴  PE=PF(全等三角形的对应边相等)

                 ∵ ∠CPD=90 ° 即 ∠CPE+∠EPD=90°

                易知∠ EPD=90 ° 即∠ DPF+∠EPF=90°

                   ∴  ∠CPE=∠DPF

              于是  在△PEC和△PFD中

                

∵

                 ∴ △PEC≌△PFD(AAS)

                  ∴  PC=PD(全等三角形的对应边相等) ………14分

 解析:略