Question

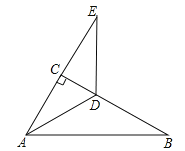
【题目】下列各小题中，都有OE平分∠AOC，OF平分∠BOC．

（1）如图①，若点A、O、B在一条直线上，∠EOF= ；

（2）如图②，若点A、O、B不在一条直线上，∠AOB=140°，则∠EOF= ；

（3）由以上两个问题发现：当∠AOC在∠BOC的外部时，∠EOF与∠AOB的数量关系是∠EOF= ；

（4）如图③，若OA在∠BOC的内部，∠AOB和∠EOF还存在上述的数量关系吗；请简单说明理由；

Answer 1

【答案】（1）90°；（2）70°；（3）∠AOB；（4）存在．

【解析】试题分析：

（1）由已知条件可得∠EOF=∠EOC+∠FOC=∠AOC+∠BOC=∠AOB=90°；

（2）由已知条件可得∠EOF=∠EOC+∠FOC=∠AOC+∠BOC=∠AOB=70°；

（3）由（1）和（2）可知，当∠AOC在∠BOC的外部时，∠EOF与∠AOB的数量关系是∠EOF=∠AOB；

（4）存在，由OE平分∠AOC，OF平分∠BOC可得∠EOC=∠AOC，∠FOC=∠BOC，结合∠BOC=∠AOC+∠AOB可得∠FOC=∠AOC+∠AOB，再由∠EOF=∠FOC-∠EOC计算可得结论.

试题解析：

（1）∵OE平分∠AOC，OF平分∠BOC，

∴∠EOC=∠AOC，∠FOC=∠BOC，

又∵∠EOF=∠EOC+∠FOC，

∴∠EOF=∠AOC+∠BOC= (∠AOC+∠BOC)= ∠AOB，

∵点A、O、B在一条直线上，

∴∠AOB=180°，

∴∠EOF=90°.

（2）∵OE平分∠AOC，OF平分∠BOC，

∴∠EOC=∠AOC，∠FOC=∠BOC，

又∵∠EOF=∠EOC+∠FOC，

∴∠EOF=∠AOC+∠BOC= (∠AOC+∠BOC)= ∠AOB，

∵∠AOB=140°，

∴∠EOF=70°.

（3）由（1）、（2）可知，∠EOF=∠AOB；

（4）存在，理由如下：

∵OE平分∠AOC，OF平分∠BOC，

∴∠EOC=∠AOC，∠FOC=∠BOC.

又∵∠EOF=∠FOC-∠EOC，

∴∠EOF=∠FOC-∠EOC= (∠BOC-∠AOC)，

又∵∠BOC-∠AOC=∠AOB，

∴∠EOF=∠AOB.