题目内容
如图，某教学楼AB后面有一座水塔CD，教学楼楼高20m，水塔高30m，教学楼
与水塔之间的距离为30m．（1）小张站在教学楼前H处，有人测得∠HDC=70°，问小张至水塔之间的距离HC是多少？
（2）如果小张身高1.70米，你认为小张在H处能越过教学楼看到水塔顶部吗？如果能看到，请说明理由；如果看不到，你认为小张至少应往前（后）走多少米？
（结果保留三个有效数字）
分析：（1）根据在直角三角形中，运用三角形的正切值来解答本题，
（2）根据平行线比例关系即可解答本题．
（2）根据平行线比例关系即可解答本题．
解答：
解：（1）∵在Rt△DCH中，∠DCH=90°，∠HDC=70°，DC=30m，tan∠HDC=
，
∴HC=DCtan70°=30tan70°≈82.4；
（2）小张在H处不能越过教学楼看到水塔顶部，
若小张往后走，设小张要往线段HC的反向延长线走xm到点I（如图），
依题意
=
，
即
=
化简，
=
1482.92+28.3x=1507.92+18.3x解得x=2.50（m），
若小张往前走，设小张要往线段HC方向走xm到点I’（如图），
依题意
=
，
即
=
，
化简，
=
1482.92-28.3x=1507，92-18.3x，
解得x=-2.50（不合题意），
答：小张至少分要向后走2.50m才能越过教学楼看到水塔顶部．
解：（1）∵在Rt△DCH中，∠DCH=90°，∠HDC=70°，DC=30m，tan∠HDC=| HC |
| DC |
∴HC=DCtan70°=30tan70°≈82.4；
（2）小张在H处不能越过教学楼看到水塔顶部，
若小张往后走，设小张要往线段HC的反向延长线走xm到点I（如图），
依题意
| IA |
| IC |
| BA-1.70 |
| DC-1.70 |
即
| 82.4-30+x |
| 82.4+x |
| 20-1.70 |
| 30-1.70 |
化简，
| 52.4+x |
| 82.4+x |
| 18.3 |
| 28.3 |
若小张往前走，设小张要往线段HC方向走xm到点I’（如图），
依题意
| I′A |
| I′C |
| BA-1.70 |
| DC-1.70 |
即
| 82.4-30-x |
| 82.4-x |
| 20-1.70 |
| 30-1.70 |
化简，
| 52.4-x |
| 82.4-x |
| 18.3 |
| 28.3 |
解得x=-2.50（不合题意），
答：小张至少分要向后走2.50m才能越过教学楼看到水塔顶部．
点评：本题考查了直角三角形正切表达式、比例关系式，考查学生考虑实际问题的能力，难度适中．
练习册系列答案
名校课堂系列答案
相关题目
，已知AF∥BC，斜坡AB长30米，坡角∠ABC=60°．改造后斜坡BE与地面成45°角，求AE至少是多少米？（精确到0.1米）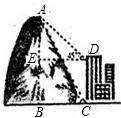
精确到0.1米，化简后再代入参数数据运算）
与水塔之间的距离为30m．