题目内容
如图1,将矩形ABCD绕点A顺时针旋转至矩形B点正好落在CD上的点E处,连结BE.
(1)求证:∠BAE=2∠CBE;
(2)如图2,连BG交AE于M,点N为BE的中点,连MN、AF,试探究AF与MN的数量关系,并证明你的结论;
(3)若AB=5,BC=3,直接写出BG的长

(1)求证:∠BAE=2∠CBE;
(2)如图2,连BG交AE于M,点N为BE的中点,连MN、AF,试探究AF与MN的数量关系,并证明你的结论;
(3)若AB=5,BC=3,直接写出BG的长
2
| 13 |
2
.| 13 |

分析:(1)求出∠ABE=∠AEB,求出∠CBE+∠ABE=90°,∠BAE+2∠ABE=180°,即可求出答案;
(2)过B作BO⊥AE于O,连接EG,根据矩形性质得出EG=AF,求出BC=BO=AG,求出M为BG中点,根据三角形中位线求出即可;
(3)根据勾股定理求出DE,求出求出OM=
DE=2,根据勾股定理求出BM,代入BG=2BM求出即可.
(2)过B作BO⊥AE于O,连接EG,根据矩形性质得出EG=AF,求出BC=BO=AG,求出M为BG中点,根据三角形中位线求出即可;
(3)根据勾股定理求出DE,求出求出OM=
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是矩形,
∴∠C=∠CBA=90°,
∴∠CBE+∠ABE=90°,
∵将矩形ABCD绕点A顺时针旋转至矩形A点正好落在CD上的点E处,
∴BC=AG,∠EAG=90°,AE=AB,
∴∠ABE=∠AEB,
∵∠BAE+∠ABE+∠AEB=180°,
∴2∠ABE+∠BAE=180°,
∵∠CBE+∠ABE=90°,
∴2∠CBE+2∠ABE=180°,
∴∠BAE=2∠CBE.
(2)MN=
AF,
证明:过B作BO⊥AE于O,连接EG,
∵四边形AEFG是矩形,
∴AF=EG,∠MAG=∠BOM=90°,
∵∠C=∠CBA=90°,
∴∠AEB=∠ABE=90°-∠CBE,∠CEB=90°-∠CBE,
∴∠CEB=∠OEB,
在△CBE和△OBE中
∴△CBE≌△OBE(AAS),
∴EC=OE,BO=BC=AD=AG,
在△BOM和△GAM中
,
∴△BOM≌△GAM(AAS),
∴BM=GM,
∵点N为BE的中点,
∴MN=
EG,
∵EG=AF,
∴MN=
AF.
(3)解:在Rt△DEA中,∠EDA=90°,AD=BC=3,AE=AB=5,由勾股定理得:DE=4,
∵△BOM≌△GAM,△CBE≌△OBE,
∴OM=AM,EC=EO,
∴OM=
=
=
=
=2,
在Rt△BOM中,由勾股定理得:BM=
=
=
∵BM=GM,
∴BG=
+
=2
,
故答案为:2
.
∴∠C=∠CBA=90°,
∴∠CBE+∠ABE=90°,
∵将矩形ABCD绕点A顺时针旋转至矩形A点正好落在CD上的点E处,
∴BC=AG,∠EAG=90°,AE=AB,
∴∠ABE=∠AEB,
∵∠BAE+∠ABE+∠AEB=180°,
∴2∠ABE+∠BAE=180°,
∵∠CBE+∠ABE=90°,
∴2∠CBE+2∠ABE=180°,
∴∠BAE=2∠CBE.

(2)MN=
| 1 |
| 2 |
证明:过B作BO⊥AE于O,连接EG,
∵四边形AEFG是矩形,
∴AF=EG,∠MAG=∠BOM=90°,
∵∠C=∠CBA=90°,
∴∠AEB=∠ABE=90°-∠CBE,∠CEB=90°-∠CBE,
∴∠CEB=∠OEB,
在△CBE和△OBE中
|
∴△CBE≌△OBE(AAS),
∴EC=OE,BO=BC=AD=AG,
在△BOM和△GAM中
|
∴△BOM≌△GAM(AAS),
∴BM=GM,
∵点N为BE的中点,
∴MN=
| 1 |
| 2 |
∵EG=AF,
∴MN=
| 1 |
| 2 |
(3)解:在Rt△DEA中,∠EDA=90°,AD=BC=3,AE=AB=5,由勾股定理得:DE=4,
∵△BOM≌△GAM,△CBE≌△OBE,
∴OM=AM,EC=EO,
∴OM=
| AE-OE |
| 2 |
=
| AB-EC |
| 2 |
=
| ED |
| 2 |
=
| 4 |
| 2 |
=2,
在Rt△BOM中,由勾股定理得:BM=
| BO2+OM2 |
| 32+22 |
| 13 |
∵BM=GM,
∴BG=
| 13 |
| 13 |
| 13 |
故答案为:2
| 13 |
点评:本题考查了勾股定理,矩形性质,旋转性质,全等三角形的性质和判定,三角形的中位线等知识点的应用,主要考查学生综合运行定理进行推理的能力,有一定的难度.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
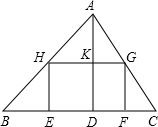 如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,种草的面积与种花的面积相等?
如图所示,某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米.学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图).其中矩形EFGH的一边EF在边BC上.其中两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,在△BHE、△GFC上都种花,在矩形EFGH上兴建喷泉.当FG长为多少米时,种草的面积与种花的面积相等?

 时,求出y的值;
时,求出y的值;
