题目内容
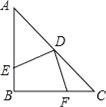
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度在边
的速度在边![]() 的延长线上运动.以
的延长线上运动.以![]() 为边作等边三角形
为边作等边三角形![]() ,点
,点![]() 在直线
在直线![]() 同侧.连结
同侧.连结![]() 相交于点
相交于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() .
.

(1)当![]()
![]() 时,
时,![]() .
.
(2)求证:![]() .
.
(3)求![]() 的度数.
的度数.
(4)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,当点
,当点![]() 将边
将边![]() 分成
分成![]() 的两部分时,直接写出
的两部分时,直接写出![]() 的周长.
的周长.
【答案】(1)2;(2)见解析;(3)![]() ;(4)
;(4)![]() 的周长为
的周长为![]() 或
或![]()
【解析】
(1)当![]() 时,两个三角形全等.
时,两个三角形全等.
(2)根据![]() 证明三角形全等即可.
证明三角形全等即可.
(3)利用全等三角形的性质解决问题即可.
(4)分两种情形:①![]() .②
.②![]() ,分别求解即可.
,分别求解即可.
(1)![]() ,
,![]() 都是等边三角形,
都是等边三角形,
![]() 当
当![]() 时,
时,![]() .
.
![]() ,
,
故答案为![]() .
.
(2)![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
(3)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() .
.
(4)如图1中,
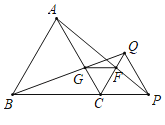
图1
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
当![]() 时,
时,![]() ,
,
![]() 的周长为
的周长为![]()
如图2中,当![]() 时,
时,![]() ,
,![]() 的周长为
的周长为![]() .
.
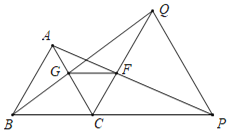
图2
综上所述,![]() 的周长为
的周长为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】保险公司车保险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
该公司随机调查了该险种的300名续保人在一年内的出险情况,得到如下统计图:

(1)样本中,保费高于基本保费的人数为__________名;
(2)已知该险种的基本保费a为6 000元,估计1名续保人本年度的平均保费.